
(本小題滿分12分)
在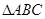 中,角
中,角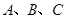 所對(duì)的邊分別為
所對(duì)的邊分別為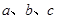 且
且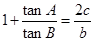 .
.
(1)求角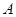 ;
;
(2)已知 ,求
,求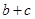 的值.
的值.
(1) (2)
(2)
解析試題分析:解:(1)由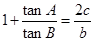 及正弦定理,得
及正弦定理,得 .........3分
.........3分
即
 ......... 5分
......... 5分
在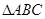 中,
中, .........6分
.........6分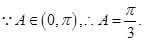 .........7分
.........7分
(2)由余弦定理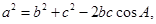 .........8分
.........8分
又
則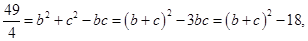 .........10分
.........10分
解得: .........12分
.........12分
考點(diǎn):考查了解三角形知識(shí)。
點(diǎn)評(píng):解題的關(guān)鍵是通過(guò)切化弦,然后得到角A的值,結(jié)合余弦定理來(lái)得到b+c的值,屬于基礎(chǔ)題。考查了分析問(wèn)題和解決問(wèn)題的能力,易錯(cuò)點(diǎn)就是對(duì)于內(nèi)角和定理的準(zhǔn)確表示變形。



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分12分)在△ABC中,BC= ,AC=3,sinC=2sinA.
,AC=3,sinC=2sinA.
(Ⅰ)求邊長(zhǎng)AB的值;
(Ⅱ)求△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
某港口O要將一件重要物品用小艇送到一艘正在航行的輪船上,在小艇出發(fā)時(shí),輪船位于港口O北偏西30°且與該港口相距20海里的A處,并正以30海里/小時(shí)的航行速度沿正東方向勻速行駛,經(jīng)過(guò)t小時(shí)與輪船相遇。
(Ⅰ)若希望相遇時(shí)小艇的航行距離最小,則小艇航行速度的大小應(yīng)為多少?
(Ⅱ)假設(shè)小艇的最高航行速度只能達(dá)到30海里/小時(shí),試設(shè)計(jì)航行方案(即確定航行方向和航行速度的大小),使得小艇能以最短時(shí)間與輪船相遇,并說(shuō)明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分12分)
如圖,飛機(jī)的航線和山頂在同一個(gè)鉛直平面內(nèi),已知飛機(jī)的高度為海拔25000米,速度為3000米/分鐘,飛行員先在點(diǎn)A看到山頂C的俯角為300,經(jīng)過(guò)8分鐘后到達(dá)點(diǎn)B,此時(shí)看到山頂C的俯角為600,則山頂?shù)暮0胃叨葹槎嗌倜祝▍⒖紨?shù)據(jù): =1.414,
=1.414, =1.732,
=1.732, =2.449).
=2.449).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分12分)已知A、B、C為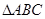 的三個(gè)內(nèi)角且向量
的三個(gè)內(nèi)角且向量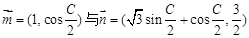 共線。
共線。
(Ⅰ)求角C的大小:
(Ⅱ)設(shè)角 的對(duì)邊分別是
的對(duì)邊分別是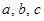 ,且滿足
,且滿足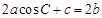 ,試判斷
,試判斷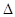
 的形狀.
的形狀.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分10分)
在 中內(nèi)角
中內(nèi)角 的對(duì)邊分別為
的對(duì)邊分別為 ,且
,且
(1)求 的值;
的值;
(2)如果b=4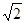 ,且a=c,求
,且a=c,求 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分12分)
已知在銳角△ABC中,a, b, c分別為角A、B、C所對(duì)的邊,向量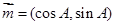 ,
,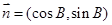 ,
,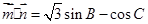 .
.
(1)求角A的大小;
(2)若a=3,求△ABC面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本題滿分10分)如圖,△ABC中,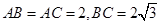 ,點(diǎn)D 在BC邊上,∠ADC=45°。
,點(diǎn)D 在BC邊上,∠ADC=45°。
(1)求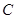 的大小;(2)求AD的長(zhǎng)。
的大小;(2)求AD的長(zhǎng)。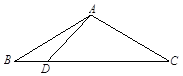
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com