
【題目】如圖,點F1 , F2分別是橢圓C:![]() 的左、右焦點.點A是橢圓C上一點,點B是直線AF2與橢圓C的另一交點,且滿足AF1⊥x軸,∠AF2F1=30°.
的左、右焦點.點A是橢圓C上一點,點B是直線AF2與橢圓C的另一交點,且滿足AF1⊥x軸,∠AF2F1=30°.
(1)求橢圓C的離心率e;
(2)若△ABF1的周長為4![]() , 求橢圓C的標準方程;
, 求橢圓C的標準方程;
(3)若△ABF1的面積為8![]() , 求橢圓C的標準方程.
, 求橢圓C的標準方程.
【答案】解:(1)Rt△AF1F2中,∵∠AF2F1=30°,
∴![]() ,
,
則![]() ,代入
,代入![]() 并利用b2=a2﹣c2化簡整理,
并利用b2=a2﹣c2化簡整理,
得3a4﹣2a2c2﹣3c4=0,即(a2﹣3c2)(3a2﹣c2)=0,
∵a>c,
∴a=![]() c,
c,
∴e=![]() =
=![]() .
.
(2)由橢圓定義知AF1+AF2=BF1+BF2=2a,
∴△ABF1的周長為4a,
∴4a=4![]() ,則a=
,則a=![]() ,b=
,b=![]() ,
,
故橢圓C的標準方程為![]() ;
;
(3)由(1)知a=![]() c,則b=
c,則b=![]() c,
c,
于是橢圓方程可化為![]() ,即2x2+3y2=6c2 ,
,即2x2+3y2=6c2 ,
設直線AF2的方程為y=![]() (x-c),代入2x2+3y2=6c2化簡整理得3x2﹣2cx﹣5c2=0,
(x-c),代入2x2+3y2=6c2化簡整理得3x2﹣2cx﹣5c2=0,
∴x=﹣c或x=![]() c,
c,
則點B的橫坐標為![]() c,
c,
∴點B到直線AF1的距離為![]() c-(-c)=
c-(-c)=![]() c
c
∴△ABF1的面積為![]() ,
,
解得c=3,
∴a=3![]() ,b=3
,b=3![]()
故橢圓C的標準方程為![]() .
.
【解析】(1)通過求解直角三角形得到A的坐標,代入橢圓方程整理,結合隱含條件求得橢圓C的離心率e;
(2)通過橢圓定義結合三角形的周長及隱含條件求得答案;
(3)由(1)得到a與c,b與c的關系,設直線AF2的方程為y=![]() (x-c),代入2x2+3y2=6c2化簡整理,求得B的坐標,再由點到直線的距離公式結合三角形面積求得答案.
(x-c),代入2x2+3y2=6c2化簡整理,求得B的坐標,再由點到直線的距離公式結合三角形面積求得答案.
【考點精析】本題主要考查了橢圓的標準方程的相關知識點,需要掌握橢圓標準方程焦點在x軸:![]() ,焦點在y軸:
,焦點在y軸:![]() 才能正確解答此題.
才能正確解答此題.


 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:高中數學 來源: 題型:
【題目】某工科院校對![]() ,
, ![]() 兩個專業的男女生人數進行調查,得到如下的列聯表:
兩個專業的男女生人數進行調查,得到如下的列聯表:
專業 | 專業 | 總計 | |
女生 | 12 | 4 | 16 |
男生 | 38 | 46 | 84 |
總計 | 50 | 50 | 100 |
(Ⅰ)從![]() 專業的女生中隨機抽取2名女生參加某項活動,其中女生甲被選到的概率是多少?
專業的女生中隨機抽取2名女生參加某項活動,其中女生甲被選到的概率是多少?
(Ⅱ)能否有95%的把握認為工科院校中“性別”與“專業”有關系?
附: 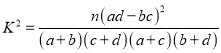 .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖(示意),公路AM、AN圍成的是一塊頂角為α的角形耕地,其中tanα=-2.在該塊土地中P處有一小型建筑,經測量,它到公路AM,AN的距離分別為3km,km.現要過點P修建一條直線公路BC,將三條公路圍成的區域ABC建成一個工業園.為盡量減少耕地占用,問如何確定B點的位置,使得該工業園區的面積最小?并求最小面積.
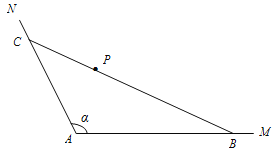
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3+ax2+bx+a2(a>0)在x=1處有極值10.
(1)求a、b的值;
(2)求f(x)的單調區間;
(3)求f(x)在[0,4]上的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,函數f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤ ![]() )的圖象與坐標軸的三個交點為P,Q,R,且P(1,0),Q(m,0)(m>0),∠PQR=
)的圖象與坐標軸的三個交點為P,Q,R,且P(1,0),Q(m,0)(m>0),∠PQR= ![]() ,M為QR的中點,|PM|=
,M為QR的中點,|PM|= ![]() .
. 
(1)求m的值及f(x)的解析式;
(2)設∠PRQ=θ,求tanθ.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正方體ABCD﹣A1B1C1D1中,E、F分別是AA1、AB的中點,則EF與對角面A1C1CA所成角的度數是( )
A.30°
B.45°
C.60°
D.150°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C1和雙曲線C2焦點相同,且離心率互為倒數,F1 , F2它們的公共焦點,P是橢圓和雙曲線在第一象限的交點,當∠F1PF2=60°時,則橢圓C1的離心率為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區有100名學員參加交通法規考試,考試成績的頻率分布直方圖如圖所示.其中成績分組區間是:第1組:[75,80),第2組:[80,85),第3組:[85,90),第4組:[90,95),第5組:[95,100].
(1)求圖中a的值,并估計此次考試成績的中位數(結果保留一位小數);
(2)在第2、4小組中用分層抽樣的方法抽取5人,再從這5人中隨機選取2人進行面試,求至少有一人來自第2小組的概率.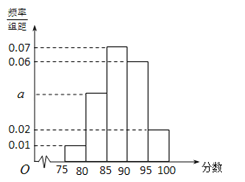
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com