
【題目】從某山區養殖場散養的3500頭豬中隨機抽取5頭,測量豬的體長x(cm)和體重y(kg),得如下測量數據:
豬編號 | 1 | 2 | 3 | 4 | 5 |
x | 169 | 181 | 166 | 185 | 180 |
y | 95 | 100 | 97 | 103 | 101 |
(1)當且僅當x,y滿足:x≥180且y≥100時,該豬為優等品,用上述樣本數據估計山區養殖場散養的3500頭豬中優等品的數量;
(2)從抽取的上述5頭豬中,隨機抽取2頭中優等品數x的分布列及其數學期望.
【答案】
(1)解:由已知隨機抽取的5頭豬中,優等品有3頭,
∴估計山區養殖場散養的3500頭豬中優等品的數量為:
3500× ![]() =2100(頭)
=2100(頭)
(2)解:∵抽取的5頭豬中,優等品有3頭,非優等品有2頭,
∴隨機抽取2頭中優等品數X的可能取值為0,1,2,
P(X=0)= ![]() =
= ![]() ,
,
P(X=1)= ![]() =
= ![]() ,
,
P(X=2)= ![]() =
= ![]() ,
,
∴X的分布列為:
X | 0 | 1 | 2 |
P |
|
|
|
EX= ![]() =
= ![]()
【解析】(1)由已知隨機抽取的5頭豬中,優等品有3頭,由此能估計山區養殖場散養的3500頭豬中優等品的數量.(2)抽取的5頭豬中,優等品有3頭,非優等品有2頭,隨機抽取2頭中優等品數X的可能取值為0,1,2,分別求出相應的概率,由此能求出X的分布列和EX.
【考點精析】解答此題的關鍵在于理解離散型隨機變量及其分布列的相關知識,掌握在射擊、產品檢驗等例子中,對于隨機變量X可能取的值,我們可以按一定次序一一列出,這樣的隨機變量叫做離散型隨機變量.離散型隨機變量的分布列:一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn,X取每一個值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,則稱表為離散型隨機變量X 的概率分布,簡稱分布列.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】連續拋擲同一顆均勻的骰子,令第i次得到的點數為ai , 若存在正整數k,使a1+a2+…+ak=6,則稱k為你的幸運數字.
(1)求你的幸運數字為3的概率;
(2)若k=1,則你的得分為5分;若k=2,則你的得分為3分;若k=3,則你的得分為1分;若拋擲三次還沒找到你的幸運數字則記0分,求得分X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數 ![]() .
.
(1)用含a的式子表示b;
(2)令F(x)= ![]() ,其圖象上任意一點P(x0 , y0)處切線的斜率
,其圖象上任意一點P(x0 , y0)處切線的斜率 ![]() 恒成立,求實數a的取值范圍;
恒成立,求實數a的取值范圍;
(3)若a=2,試求f(x)在區間 ![]() 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,CA,CB分別與圓O切于A,B兩點,AE是直徑,OF平分∠BOE交CB的延長線于F,BD∥AC. 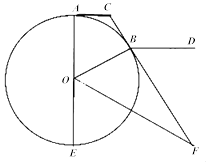
(1)證明:OB2=BCBF;
(2)證明:∠DBF=∠AOB.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】拋物線![]() 的焦點為
的焦點為![]() 上任一點
上任一點![]() 在
在![]() 軸上的射影為
軸上的射影為![]() 中點為
中點為![]() ,
,![]() .
.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)直線![]() 過
過![]() 與
與![]() 從下到上依次交于
從下到上依次交于![]() ,與
,與![]() 交于
交于![]() ,直線
,直線![]() 過
過![]() 與
與![]() 從下到上依次交于
從下到上依次交于![]() ,與
,與![]() 交于
交于![]() ,
,![]() ,
,![]() 的斜率之積為
的斜率之積為![]() ,設
,設![]() 的面積分別為
的面積分別為![]() ,是否存在
,是否存在![]() 使得
使得![]() 成等比數列?若存在,求
成等比數列?若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 、
、![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點.
的左、右焦點.
(1)若![]() 是該橢圓上的一個動點,求
是該橢圓上的一個動點,求![]() 的最大值和最小值;
的最大值和最小值;
(2)設過定點![]() 的直線與橢圓交于不同的兩點
的直線與橢圓交于不同的兩點![]() 、
、![]() ,且
,且![]() 為銳角(其中
為銳角(其中![]() 為坐標原點),求直線
為坐標原點),求直線![]() 的斜率
的斜率![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C1:x2=y,圓C2:x2+(y﹣4)2=1的圓心為點M
(1)求點M到拋物線C1的準線的距離;
(2)已知點P是拋物線C1上一點(異于原點),過點P作圓C2的兩條切線,交拋物線C1于A,B兩點,若過M,P兩點的直線l垂直于AB,求直線l的方程.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com