為了解某班學生喜愛打籃球是否與性別有關，對本班50人進行了問卷調查得到了如下列表：
| | 喜愛打籃球 | 不喜愛打籃球 | 合計 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合計 | | | 50 |
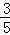．| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
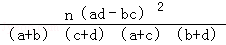，其中n=a+b+c+d） （1）
（2）在犯錯誤的概率不超過0.005的前提下，認為喜愛打籃球與性別有關． 喜愛打籃球 不喜愛打籃球 合計 男生 20 5 25 女生 10 15 25 合計 30 20 50
（3）ξ 0 1 2 P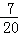 
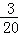
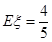
解析試題分析：（1）因為隨機抽取1人抽到喜愛打籃球的學生的概率為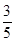
，所以喜愛打籃球的學生人數為
，則不喜愛打籃球的學生人數為
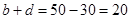，由表可得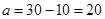
，
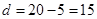，因此調查的人數中男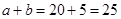生有
，女生有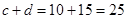
.
（2）由（1）得到的數據代入公式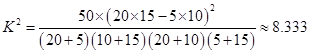
，比對臨界值表，因為
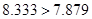，所以可以在犯錯的概率不超過0.005的前提下，人為喜愛打籃球與性別無關.
（3）由（1）知調查的女生人數為25名，其中喜愛打籃球的女生人數為10名，從女生中抽取2名，則可以確定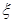
的值為0、1、2，根據古典概型計算公式得
，
，
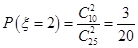，從而可列出所求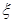的分布列,再根據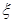的分布列求出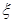的期望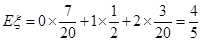
.
試題解析：（1）列聯表補充如下： （3分）
（2）∵K2= 喜愛打籃球 不喜愛打籃球 合計 男生 20 5 25 女生 10 15 25 合計 30 20 50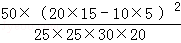 
≈8.333＞7.879 （5分）
∴在犯錯誤的概率不超過0.005的前提下，認為喜愛打籃球與性別有關． （6分）
（3）喜愛打籃球的女生人數ξ的可能取值為0，1，2． （7分）
其概率分別為P（ξ=0）=
，P（ξ=1）=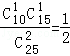
，P（ξ=2）=
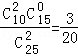（10分）
故ξ的分布列為：
名同學,現測得排球隊
)分別是:
、
、
、
、
、
、
、
、
、
、
、
、
、
、
、
,求
表示進入商場的3位顧客中至少購買甲、乙兩種商品中的一種的人數，求
，求隨機變量
，求隨機變量
的函數：
，
，
，
，
，
.
的分布列和數學期望．
,
,
,
,
五個等級.現從一批該產品隨機抽取20個，對其等級進行統計分析，得到頻率分布表如下： 
