
【題目】已知橢圓![]() 過點
過點![]() ,離心率為
,離心率為![]() .若
.若![]() 是橢圓
是橢圓![]() 上的不同的兩點,
上的不同的兩點, ![]() 的面積記為
的面積記為![]() .
.
(I)求橢圓![]() 的方程;
的方程;
(II)設直線![]() 的方程為
的方程為![]() ,
, ![]() ,
, ![]() ,求
,求![]() 的值;
的值;
(III)設直線![]() ,
, ![]() 的斜率之積等于
的斜率之積等于![]() ,試證明:無論
,試證明:無論![]() 如何移動,面積
如何移動,面積![]() 保持不變.
保持不變.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)詳見解析.
;(III)詳見解析.
【解析】試題分析:(I)利用![]() 列方程,求出
列方程,求出![]() 的值,由此得到橢圓方程.(II)聯立直線
的值,由此得到橢圓方程.(II)聯立直線![]() 的方程和橢圓方程,求得交點坐標,利用點到直線距離公式求得三角形的高,由此得到三角形面積的表達式,并由此求得
的方程和橢圓方程,求得交點坐標,利用點到直線距離公式求得三角形的高,由此得到三角形面積的表達式,并由此求得![]() 的值.(III)設出直線
的值.(III)設出直線![]() 的方程,聯立直線的方程和橢圓的方程,寫出韋達定理,代入向量運算
的方程,聯立直線的方程和橢圓的方程,寫出韋達定理,代入向量運算![]() ,利用弦長公式和點到直線距離公式求得面積的表達式,化簡得到面積保持不變.
,利用弦長公式和點到直線距離公式求得面積的表達式,化簡得到面積保持不變.
試題解析:
(I)由題知 ,
,
解得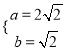 ,
,
所以橢圓![]() 的方程為
的方程為![]() .
.
(II)法1:由 得
得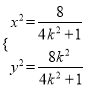 點
點![]() 到直線
到直線![]() 的距離
的距離![]() 所以
所以![]() 的面積
的面積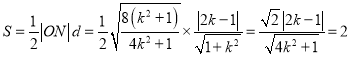 即
即![]() 解得
解得![]()
(III)橢圓方程為![]() ,
,
過![]() 兩點的直線
兩點的直線![]() 的方程
的方程![]() ,其中
,其中![]() ,
, ![]() ,
,
則![]() ,
,
得![]() ,
,
![]() ,
,![]() ,
,
因為![]() ,
,
所以![]() .
.
則![]() ,
,
坐標原點到直線![]() 的距離為
的距離為![]() ,
,
所以![]() ,
,
所以無論![]() 如何移動,面積
如何移動,面積![]() 保持不變.
保持不變. ![]() 的值為
的值為![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD的底面ABCD為矩形,PA⊥平面ABCD,點E是棱PD的中點,點F是PC的中點F. 
(1)證明:PB∥平面AEC;
(2)若ABCD為正方形,探究在什么條件下,二面角C﹣AF﹣D大小為60°?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,△ABC內接于直徑為BC的圓O,過點A作圓O的切線交CB的延長線于點P,∠BAC的平分線分別交BC和圓O于點D、E,若PA=2PB=10. 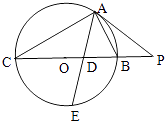
(1)求證:AC=2AB;
(2)求ADDE的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在2007全運會上兩名射擊運動員甲、乙在比賽中打出如下成績:
甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;
乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;
(1)用莖葉圖表示甲,乙兩個成績;并根據莖葉圖分析甲、乙兩人成績;
(2)分別計算兩個樣本的平均數![]() 和標準差
和標準差![]() ,并根據計算結果估計哪位運動員的成績比較穩定.
,并根據計算結果估計哪位運動員的成績比較穩定.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l: ![]() (t為參數,α≠0)經過橢圓C:
(t為參數,α≠0)經過橢圓C: ![]() (φ為參數)的左焦點F.
(φ為參數)的左焦點F.
(1)求實數m的值;
(2)設直線l與橢圓C交于A、B兩點,求|FA|×|FB|取最小值時,直線l的傾斜角α.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com