
【題目】已知函數(shù)f(x)=lnx﹣x2+ax,a∈R.
(Ⅰ)證明lnx≤x﹣1;
(Ⅱ)若a≥1,討論函數(shù)f(x)的零點個數(shù).
【答案】(Ⅰ)見解析(Ⅱ)見解析
【解析】
(Ⅰ)令![]() 進而求導求最值即可證得;
進而求導求最值即可證得;
(Ⅱ)求函數(shù)導數(shù),分析單調(diào)性,由f(1>0,![]() 及
及![]() ,利用零點存在定理即可得解.
,利用零點存在定理即可得解.
(Ⅰ)證明:令![]() ,
,
可得:x∈(0,1)時,g′(x)>0,函數(shù)g(x)單調(diào)遞增;x∈(1,+∞)時,g′(x)<0,函數(shù)g(x)單調(diào)遞減.
∴可得x=1時,函數(shù)g(x)取得極大值即最大值,∴g(x)≤g(1)=0,即lnx≤x﹣1.
(II)解:根據(jù)題意,![]() .
.
令![]() ,解得
,解得![]() ,(負值舍去),
,(負值舍去),
在(0,x0)上,![]() ,函數(shù)f(x)單調(diào)遞增;在(x0,+∞)上,
,函數(shù)f(x)單調(diào)遞增;在(x0,+∞)上,![]() ,函數(shù)f(x)單調(diào)遞減.
,函數(shù)f(x)單調(diào)遞減.
∴f(x)max=f(x0).
當a=1時,x0=1,f(x)max=f(1)=0,此時函數(shù)f(x)只有一個零點1.
當a>1時,![]() ,f(1)=a﹣1>0,
,f(1)=a﹣1>0,![]() .
.
![]() .
.
∴函數(shù)f(x)在區(qū)間![]() 和區(qū)間(1,2a)上各有一個零點.
和區(qū)間(1,2a)上各有一個零點.
綜上可得:當a=1時,函數(shù)f(x)只有一個零點1.
當a>1時,函數(shù)f(x)有兩個零點.


科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若![]() 在
在![]() 上為單調(diào)遞增,求實數(shù)
上為單調(diào)遞增,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若![]() ,且
,且![]() ,求證:對定義域內(nèi)的任意實數(shù)
,求證:對定義域內(nèi)的任意實數(shù)![]() ,不等式
,不等式![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若![]() ,求函數(shù)
,求函數(shù)![]() 在區(qū)間
在區(qū)間![]() (其中
(其中![]() ,
,![]() 是自然對數(shù)的底數(shù))上的最小值;
是自然對數(shù)的底數(shù))上的最小值;
(2)若存在與函數(shù)![]() ,
,![]() 的圖象都相切的直線,求實數(shù)
的圖象都相切的直線,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了解某校學生參加社區(qū)服務(wù)的情況,采用按性別分層抽樣的方法進行調(diào)查.已知該校共有學生960人,其中男生560人,從全校學生中抽取了容量為![]() 的樣本,得到一周參加社區(qū)服務(wù)的時間的統(tǒng)計數(shù)據(jù)好下表:
的樣本,得到一周參加社區(qū)服務(wù)的時間的統(tǒng)計數(shù)據(jù)好下表:
超過1小時 | 不超過1小時 | |
男 | 20 | 8 |
女 | 12 | m |
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)能否有95%的把握認為該校學生一周參加社區(qū)服務(wù)時間是否超過1小時與性別有關(guān)?
(Ⅲ)以樣本中學生參加社區(qū)服務(wù)時間超過1小時的頻率作為該事件發(fā)生的概率,現(xiàn)從該校學生中隨機調(diào)查6名學生,試估計6名學生中一周參加社區(qū)服務(wù)時間超過1小時的人數(shù).
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某公司為了提高利潤,從2014年至2018年每年對生產(chǎn)環(huán)節(jié)的改進進行投資,投資金額與年利潤增長的數(shù)據(jù)如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
投資金額x(萬元) | 5 | 5.5 | 6 | 6.5 | 7 |
年利潤增長y(萬元) | 7.5 | 8 | 9 | 10 | 11.5 |
(1)請用最小二乘法求出y關(guān)于x的回歸直線方程;
(2)如果2020年該公司計劃對生產(chǎn)環(huán)節(jié)的改進的投資金額為8萬元,估計該公司在該年的年利潤增長為多少?
參考公式: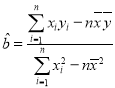 ,
,![]() 參考數(shù)據(jù):
參考數(shù)據(jù):![]() ,
,![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ,
,![]() ,
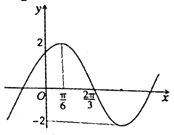
,![]() )的圖象如圖所示,令
)的圖象如圖所示,令![]() ,則下列關(guān)于函數(shù)
,則下列關(guān)于函數(shù)![]() 的說法中正確的是( )
的說法中正確的是( )
A. 函數(shù)![]() 圖象的對稱軸方程為
圖象的對稱軸方程為![]()
![]()
B. 函數(shù)![]() 的最大值為2
的最大值為2
C. 函數(shù)![]() 的圖象上存在點
的圖象上存在點![]() ,使得在
,使得在![]() 點處的切線與直線
點處的切線與直線![]() 平行
平行
D. 若函數(shù)![]() 的兩個不同零點分別為
的兩個不同零點分別為![]() ,
,![]() ,則
,則![]() 最小值為
最小值為![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,多面體ABCDEF中,四邊形ABCD為矩形,二面角A-CD-F為60°,DE∥CF,CD⊥DE,AD=2,DE=DC=3,CF=6.

(1)求證:BF∥平面ADE;
(2)在線段CF上求一點G,使銳二面角B-EG-D的余弦值為![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)點P,Q分別是曲線y=xe﹣x(e是自然對數(shù)的底數(shù))和直線y=x+3上的動點,則P,Q兩點間距離的最小值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com