
 是等差數(shù)列,且
是等差數(shù)列,且 且
且 成等比數(shù)列。
成等比數(shù)列。 的通項公式
的通項公式 ,求前n項和
,求前n項和 .
.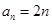 ;(2)
;(2)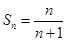 .
.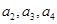 展開,通過解方程,解出基本量
展開,通過解方程,解出基本量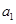 和
和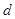 ,而此題
,而此題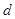 有2個值,需通過已知條件驗證舍掉一個,從而得到等差數(shù)列的通項公式;第二問,利用第一問的結(jié)論,代入到
有2個值,需通過已知條件驗證舍掉一個,從而得到等差數(shù)列的通項公式;第二問,利用第一問的結(jié)論,代入到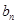 中,用裂項相消法求和.
中,用裂項相消法求和. 的公差為
的公差為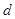 ,又
,又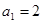
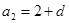 ,
,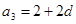 ,
,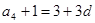 ,
,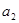 ,
,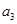 ,
,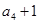 成等比數(shù)列.
成等比數(shù)列.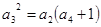 ,即
,即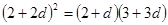 ,
,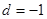 或
或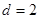 , 4分
, 4分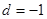 時,
時,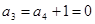 ,與
,與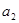 ,
,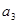 ,
,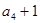 成等比數(shù)列矛盾,
成等比數(shù)列矛盾,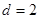 ,∴
,∴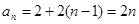 ,即
,即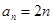 . 6分
. 6分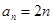 ,∴
,∴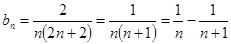 8分
8分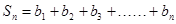
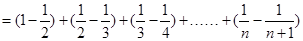
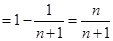 .
.

 期末沖刺100分創(chuàng)新金卷完全試卷系列答案
期末沖刺100分創(chuàng)新金卷完全試卷系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
 滿足
滿足 (
( ).
).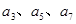 的值;
的值; (用含
(用含 的式子表示);
的式子表示); ,數(shù)列
,數(shù)列
 的前
的前 項和為
項和為 ,求
,求 (用含
(用含 的式子表示).).
的式子表示).).查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
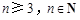 )項,且
)項,且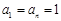 ,對每個i (1≤i≤
,對每個i (1≤i≤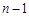 ,i
,i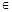 N),均有
N),均有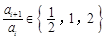 .
.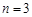 時,寫出滿足條件的所有數(shù)列{an}(不必寫出過程);
時,寫出滿足條件的所有數(shù)列{an}(不必寫出過程);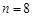 時,求滿足條件的數(shù)列{an}的個數(shù).
時,求滿足條件的數(shù)列{an}的個數(shù).查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 中,已知
中,已知 .
. 的通項公式;
的通項公式; 分別為等差數(shù)列
分別為等差數(shù)列 的第3項和第5項,試求數(shù)列
的第3項和第5項,試求數(shù)列 的通項公式及前
的通項公式及前 項和
項和 。
。查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
| A.-48 |
| B.-40 |
| C.-49 |
| D.-43 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
 間的整數(shù)
間的整數(shù) 為分子,以
為分子,以 為分母組成分數(shù)集合
為分母組成分數(shù)集合 ,其所有元素和為
,其所有元素和為 ;以
;以 間的整數(shù)
間的整數(shù) 為分子,以
為分子,以 為分母組成不屬于集合
為分母組成不屬于集合 的分數(shù)集合
的分數(shù)集合 ,其所有元素和為
,其所有元素和為 ;……,依次類推以
;……,依次類推以 間的整數(shù)
間的整數(shù) 為分子,以
為分子,以 為分母組成不屬于
為分母組成不屬于 的分數(shù)集合
的分數(shù)集合 ,其所有元素和為
,其所有元素和為 ;則
;則 =________.
=________.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
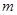 行:
行: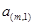
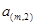
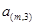
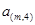
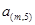 ………………
………………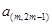
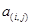 表示第
表示第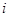 行中的第
行中的第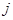 個數(shù))
個數(shù))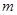 行的數(shù)的和是_________________.
行的數(shù)的和是_________________.查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com