
【題目】設函數(shù)![]()
![]() ,e為自然對數(shù)的底數(shù).
,e為自然對數(shù)的底數(shù).
(1)求f(x)的單調(diào)區(qū)間:
(2)若ax2+x+a﹣exx+exlnx≤0成立,求正實數(shù)a的取值范圍.
【答案】(1)![]() 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為![]() ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為![]() ,
,![]() ;(2)0<a
;(2)0<a![]() .
.
【解析】
(1)求導得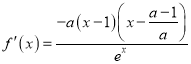 ,求得
,求得![]() 、
、![]() 的解集即可得解;
的解集即可得解;
(2)ax2+x+a﹣exx+exlnx≤0成立![]() x﹣lnx,由(1)可得當x=1時,函數(shù)y
x﹣lnx,由(1)可得當x=1時,函數(shù)y![]() 取得極大值
取得極大值![]() ,令g(x)=x﹣lnx,(x>0),利用導數(shù)研究其單調(diào)性即可得出x﹣lnx≥1.進而得出a的取值范圍.
,令g(x)=x﹣lnx,(x>0),利用導數(shù)研究其單調(diào)性即可得出x﹣lnx≥1.進而得出a的取值范圍.
(1)函數(shù)![]() ,e為自然對數(shù)的底數(shù),
,e為自然對數(shù)的底數(shù),
則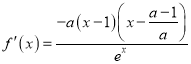 ,
,
令![]() 可得
可得![]() ,
,![]() ,
,
∴當![]() ,
,![]() 時,
時,![]() ,
,![]() 單調(diào)遞減;
單調(diào)遞減;
當![]() 時,
時,![]() ,
,![]() 單調(diào)遞增;
單調(diào)遞增;
∴![]() 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為![]() ,單調(diào)減區(qū)間為
,單調(diào)減區(qū)間為![]() ,
,![]() ;
;
(2)ax2+x+a﹣exx+exlnx≤0成立![]() x﹣lnx,x∈(0,+∞),
x﹣lnx,x∈(0,+∞),
由(1)可得當x=1函數(shù)y![]() 取得極大值
取得極大值![]() ,
,
令g(x)= x﹣lnx,(x>0),g′(x)= 1![]() ,
,
可得x=1時,函數(shù)g(x)取得極小值即最小值.
∴x﹣lnx≥g(1)=1,
當![]() 時,
時,![]() 即為函數(shù)y
即為函數(shù)y![]() 的最大值,
的最大值,
∴![]() x﹣lnx成立
x﹣lnx成立![]() 1,解得a
1,解得a![]() ;
;
當![]() 時,
時,![]() ,不合題意;
,不合題意;
綜上所述,0<a![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】中國有十二生肖,又叫十二屬相,是以十二種動物(鼠、牛、虎、兔、龍、蛇、馬、羊、猴、雞、狗、豬)形象化代表人的出生年份,現(xiàn)有十二生肖的吉祥物各一個,三位屬相不同的小朋友依次每人選一個,則三位小朋友都不選和自己屬相相同的吉祥物的選法有________種.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,拋物線
中,拋物線![]() 的焦點為
的焦點為![]() ,點
,點![]() 是拋物線
是拋物線![]() 上一點,且
上一點,且![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 為拋物線
為拋物線![]() 上異于
上異于![]() 的兩點,且
的兩點,且![]() .記點
.記點![]() 到直線
到直線![]() 的距離分別為
的距離分別為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某醫(yī)藥開發(fā)公司實驗室有![]() 瓶溶液,其中
瓶溶液,其中![]() 瓶中有細菌
瓶中有細菌![]() ,現(xiàn)需要把含有細菌
,現(xiàn)需要把含有細菌![]() 的溶液檢驗出來,有如下兩種方案:
的溶液檢驗出來,有如下兩種方案:
方案一:逐瓶檢驗,則需檢驗![]() 次;
次;
方案二:混合檢驗,將![]() 瓶溶液分別取樣,混合在一起檢驗,若檢驗結(jié)果不含有細菌
瓶溶液分別取樣,混合在一起檢驗,若檢驗結(jié)果不含有細菌![]() ,則
,則![]() 瓶溶液全部不含有細菌
瓶溶液全部不含有細菌![]() ;若檢驗結(jié)果含有細菌
;若檢驗結(jié)果含有細菌![]() ,就要對這
,就要對這![]() 瓶溶液再逐瓶檢驗,此時檢驗次數(shù)總共為
瓶溶液再逐瓶檢驗,此時檢驗次數(shù)總共為![]() .
.
(1)假設![]() ,采用方案一,求恰好檢驗3次就能確定哪兩瓶溶液含有細菌
,采用方案一,求恰好檢驗3次就能確定哪兩瓶溶液含有細菌![]() 的概率;
的概率;
(2)現(xiàn)對![]() 瓶溶液進行檢驗,已知每瓶溶液含有細菌
瓶溶液進行檢驗,已知每瓶溶液含有細菌![]() 的概率均為
的概率均為![]() .
.
若采用方案一.需檢驗的總次數(shù)為![]() ,若采用方案二.需檢驗的總次數(shù)為
,若采用方案二.需檢驗的總次數(shù)為![]() .
.
(i)若![]() 與
與![]() 的期望相等.試求
的期望相等.試求![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式
的函數(shù)解析式![]() ;
;
(ii)若![]() ,且采用方案二總次數(shù)的期望小于采用方案一總次數(shù)的期望.求
,且采用方案二總次數(shù)的期望小于采用方案一總次數(shù)的期望.求![]() 的最大值.
的最大值.
參考數(shù)據(jù):![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某企業(yè)引進現(xiàn)代化管理體制,生產(chǎn)效益明顯提高.2018年全年總收入與2017年全年總收入相比增長了一倍,實現(xiàn)翻番.同時該企業(yè)的各項運營成本也隨著收入的變化發(fā)生了相應變化.下圖給出了該企業(yè)這兩年不同運營成本占全年總收入的比例,下列說法正確的是( )
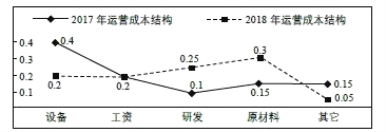
A.該企業(yè)2018年原材料費用是2017年工資金額與研發(fā)費用的和
B.該企業(yè)2018年研發(fā)費用是2017年工資金額、原材料費用、其它費用三項的和
C.該企業(yè)2018年其它費用是2017年工資金額的![]()
D.該企業(yè)2018年設備費用是2017年原材料的費用的兩倍
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖1,在邊長為2的等邊△ABC中,D,E分別為邊AC,AB的中點.將△ADE沿DE折起,使得AB⊥AD,得到如圖2的四棱錐A﹣BCDE,連結(jié)BD,CE,且BD與CE交于點H.
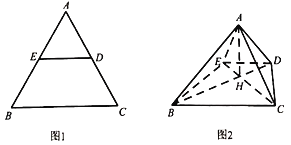
(1)證明:![]() ;
;
(2)設點B到平面AED的距離為h1,點E到平面ABD的距離為h2,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2020年是我國全面建成小康社會和“十三五”規(guī)劃收官之年,也是佛山在經(jīng)濟總量超萬億元新起點上開啟發(fā)展新征程的重要歷史節(jié)點.作為制造業(yè)城市,佛山一直堅持把創(chuàng)新擺在制造業(yè)發(fā)展全局的前置位置和核心位置,聚焦打造成為面向全球的國家制造業(yè)創(chuàng)新中心,走“世界科技+佛山智造+全球市場”的創(chuàng)新發(fā)展之路.在推動制造業(yè)高質(zhì)量發(fā)展的大環(huán)境下,佛山市某工廠統(tǒng)籌各類資源,進行了積極的改革探索.下表是該工廠每月生產(chǎn)的一種核心產(chǎn)品的產(chǎn)量![]() (件)與相應的生產(chǎn)總成本
(件)與相應的生產(chǎn)總成本![]() (萬元)的四組對照數(shù)據(jù).
(萬元)的四組對照數(shù)據(jù).
| 5 | 7 | 9 | 11 |
| 200 | 298 | 431 | 609 |
工廠研究人員建立了![]() 與
與![]() 的兩種回歸模型,利用計算機算得近似結(jié)果如下:
的兩種回歸模型,利用計算機算得近似結(jié)果如下:
模型①:![]() ;
;
模型②:![]() .
.
其中模型①的殘差(實際值預報值)圖如圖所示:
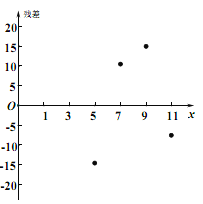
(1)根據(jù)殘差分析,判斷哪一個更適宜作為![]() 關(guān)于
關(guān)于![]() 的回歸方程?并說明理由;
的回歸方程?并說明理由;
(2)市場前景風云變幻,研究人員統(tǒng)計了20個月的產(chǎn)品銷售單價,得到頻數(shù)分布表如下:
銷售單價分組(萬元) |
|
|
|
頻數(shù) | 10 | 6 | 4 |
若以這20個月銷售單價的平均值定為今后的銷售單價(同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表),結(jié)合你對(1)的判斷,當月產(chǎn)量為12件時,預測當月的利潤.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某企業(yè)新研發(fā)了一種產(chǎn)品,產(chǎn)品的成本由原料成本及非原料成本組成.每件產(chǎn)品的非原料成本![]() (元)與生產(chǎn)該產(chǎn)品的數(shù)量
(元)與生產(chǎn)該產(chǎn)品的數(shù)量![]() (千件)有關(guān),經(jīng)統(tǒng)計得到如下數(shù)據(jù):
(千件)有關(guān),經(jīng)統(tǒng)計得到如下數(shù)據(jù):
x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y | 112 | 61 | 44.5 | 35 | 30.5 | 28 | 25 | 24 |
根據(jù)以上數(shù)據(jù),繪制了散點圖.觀察散點圖,兩個變量不具有線性相關(guān)關(guān)系,現(xiàn)考慮用反比例函數(shù)模型![]() 和指數(shù)函數(shù)模型
和指數(shù)函數(shù)模型![]() 分別對兩個變量的關(guān)系進行擬合,已求得:用指數(shù)函數(shù)模型擬合的回歸方程為
分別對兩個變量的關(guān)系進行擬合,已求得:用指數(shù)函數(shù)模型擬合的回歸方程為![]() ,
,![]() 與
與![]() 的相關(guān)系數(shù)
的相關(guān)系數(shù)![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,(其中
,(其中![]() );
);
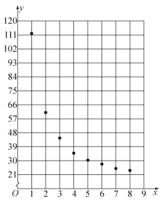
(1)用反比例函數(shù)模型求![]() 關(guān)于
關(guān)于![]() 的回歸方程;
的回歸方程;
(2)用相關(guān)系數(shù)判斷上述兩個模型哪一個擬合效果更好(精確到0.01),并用其估計產(chǎn)量為10千件時每件產(chǎn)品的非原料成本.
參考數(shù)據(jù):![]() ,
,![]()
參考公式:對于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: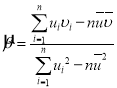 ,
,![]() ,相關(guān)系數(shù)
,相關(guān)系數(shù) .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com