
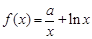 ,
,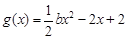 ,
,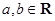
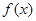 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;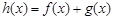 ,當
,當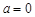 時,
時,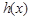 在
在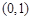 上有且只有一個極值點,求實數(shù)
上有且只有一個極值點,求實數(shù)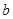 的取值范圍;
的取值范圍;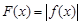 ,證明:存在一條過原點的直線
,證明:存在一條過原點的直線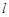 與
與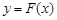 的圖象有兩個切點
的圖象有兩個切點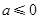 時,
時, 為單調(diào)增區(qū)間,當
為單調(diào)增區(qū)間,當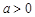 時,
時, 為單調(diào)減區(qū)間,
為單調(diào)減區(qū)間, 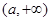 為單調(diào)增區(qū)間.
為單調(diào)增區(qū)間.
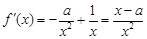 ,
, 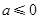 ,則
,則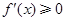 ,
,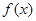 在
在 上為增函數(shù),2分 ②若
上為增函數(shù),2分 ②若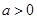 ,令
,令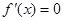 ,得
,得 ,
, 時,
時, ;當
;當 時,
時,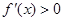 .
. 為單調(diào)減區(qū)間,
為單調(diào)減區(qū)間,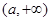 為單調(diào)增區(qū)間. 綜上可得,當
為單調(diào)增區(qū)間. 綜上可得,當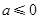 時,
時, 為單調(diào)增區(qū)間,
為單調(diào)增區(qū)間,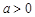 時,
時, 為單調(diào)減區(qū)間,
為單調(diào)減區(qū)間, 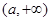 為單調(diào)增區(qū)間. 4分
為單調(diào)增區(qū)間. 4分 時,
時,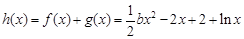 ,
, , 5分
, 5分 在
在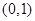 上有且只有一個極值點,即
上有且只有一個極值點,即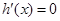 在
在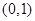 上有且只有一個根且不為重根,
上有且只有一個根且不為重根, 得
得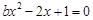 ,
, 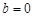 ,
, ,滿足題意;…… 6分
,滿足題意;…… 6分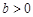 時,
時,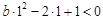 ,即
,即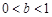 ;… 7分
;… 7分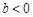 時,
時,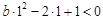 ,得
,得 ,故
,故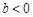 ; 綜上得:
; 綜上得: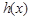 在
在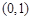 上有且只有一個極值點時,
上有且只有一個極值點時, . ………8分注:本題也可分離變量求得.
. ………8分注:本題也可分離變量求得.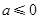 ,則
,則 ,
,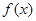 在
在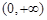 上為單調(diào)增函數(shù),
上為單調(diào)增函數(shù), 與
與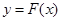 的圖象不可能有兩個切點,不合題意. 9分
的圖象不可能有兩個切點,不合題意. 9分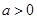 ,
,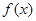 在
在 處取得極值
處取得極值 .
.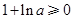 ,
,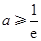 時,由圖象知不可能有兩個切點.10分
時,由圖象知不可能有兩個切點.10分 ,設
,設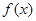 圖象與
圖象與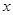 軸的兩個交點的橫坐標為
軸的兩個交點的橫坐標為 (不妨設
(不妨設 ),
),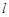 與
與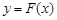 的圖象有兩個切點即為直線
的圖象有兩個切點即為直線 與
與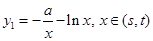 和
和 的切點.
的切點. ,
, ,
, ,則
,則 ,且
,且 ,
,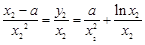 ,
,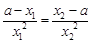 ,
, 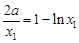 ① ,
① , 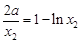 ② ,
② ,  ③ ,
③ ,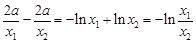 ,
, 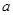 代入上式可得:
代入上式可得: ,即
,即 ,12分
,12分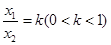 ,則
,則 ,令
,令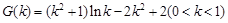 ,因為
,因為 ,
,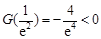 ,故存在
,故存在 ,使得
,使得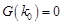 ,
,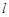 與
與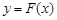 的圖象有兩個切點.14分
的圖象有兩個切點.14分

科目:高中數(shù)學 來源:不詳 題型:解答題
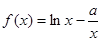 (
(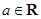 ).
).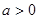 時,判斷
時,判斷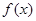 在定義域上的單調(diào)性;
在定義域上的單調(diào)性;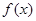 在
在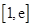 上的最小值為
上的最小值為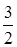 ,求
,求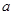 的值;
的值;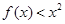 在
在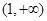 上恒成立,試求
上恒成立,試求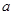 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
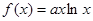 圖像上點
圖像上點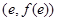 處的切線與直線
處的切線與直線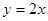 平行(其中
平行(其中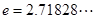 ),
),
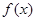 的解析式;
的解析式;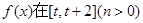 上的最小值;
上的最小值;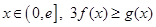 恒成立,求實數(shù)
恒成立,求實數(shù)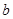 的取值范圍。
的取值范圍。查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
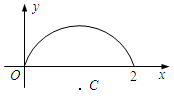
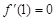 ;②
;②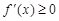 ;③
;③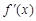 為減函數(shù);④若
為減函數(shù);④若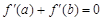 ,則a+b=2.
,則a+b=2.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
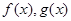 分別是定義在R上的奇函數(shù)和偶函數(shù),當
分別是定義在R上的奇函數(shù)和偶函數(shù),當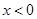 時,
時,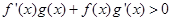 ,且g(-3)=0,則不等式
,且g(-3)=0,則不等式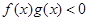 的解集是 ( )
的解集是 ( )| A.(-3,0)∪(3,+∞) | B. (-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D.(-∞,-3)∪(0,3) |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
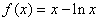 ,
,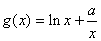 ,(
,(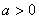 ).
).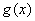 的極值;
的極值;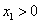 ,函數(shù)
,函數(shù)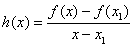 ,
, 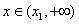 ,判斷并證明
,判斷并證明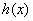 的單調(diào)性;
的單調(diào)性;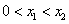 ,試比較
,試比較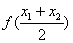 與
與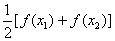 ,并加以證明.
,并加以證明.查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com