
已知函數(shù)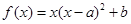 在
在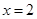 處有極大值.
處有極大值.
(Ⅰ)求 的值;
的值;
(Ⅱ)若過原點(diǎn)有三條直線與曲線 相切,求
相切,求 的取值范圍;
的取值范圍;
(Ⅲ)當(dāng)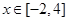 時(shí),函數(shù)
時(shí),函數(shù) 的圖象在拋物線
的圖象在拋物線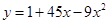 的下方,求
的下方,求 的取值范圍.
的取值范圍.
(Ⅰ)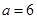 (Ⅱ)
(Ⅱ)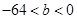 (Ⅲ)
(Ⅲ)
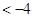
解析試題分析:(Ⅰ)通過對(duì)函數(shù)f(x)求導(dǎo),根據(jù)函數(shù)在x=2處有極值,可知f'(2)=0,解得a的值.
(Ⅱ)把(1)求得的a代入函數(shù)關(guān)系式,設(shè)切點(diǎn)坐標(biāo),進(jìn)而根據(jù)導(dǎo)函數(shù)可知切線斜率,則切線方程可得,整理可求得b的表達(dá)式,令g'(x)=0解得x1和x2.進(jìn)而可列出函數(shù)g(x)的單調(diào)性進(jìn)而可知-64<b<0時(shí),方程b=g(x)有三個(gè)不同的解,結(jié)論可得.
(Ⅲ)當(dāng)x∈[-2,4]時(shí),函數(shù)y=f(x)的圖象在拋物線y=1+45x-9x2的下方,進(jìn)而可知x3-12x2+36x+b<1+45x-9x2在x∈[-2,4]時(shí)恒成立,整理可得關(guān)于b的不等式,令h(x)=-x3+3x2+9x+1,對(duì)h(x)進(jìn)行求導(dǎo)由h'(x)=0得x1和x2.分別求得h,h(-1),h(3),h(4),進(jìn)而可知h(x)在[-2,4]上的最小值是,進(jìn)而求得b的范圍.
試題解析:(Ⅰ)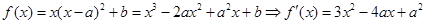 ,
,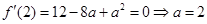 或
或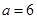 ,
,
當(dāng) 時(shí),函數(shù)在
時(shí),函數(shù)在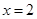 處取得極小值,舍去;
處取得極小值,舍去;
當(dāng)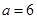 時(shí),
時(shí),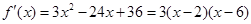 ,函數(shù)在
,函數(shù)在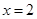 處取得極大值,符合題意,∴
處取得極大值,符合題意,∴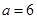 .(3分)
.(3分)
(Ⅱ)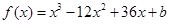 ,設(shè)切點(diǎn)為
,設(shè)切點(diǎn)為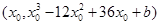 ,則切線斜率為
,則切線斜率為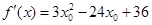 ,切線方程為
,切線方程為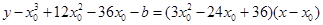 ,
,
即 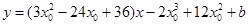 ,
,
∴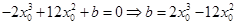 .
.
令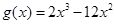 ,則
,則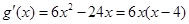 ,
,
由 得,
得,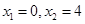 .
.
函數(shù) 的單調(diào)性如下:
的單調(diào)性如下: