【題目】如圖，四邊形
是邊長為4的正方形，點
為
邊上任意一點（與點
不重合），連接
，過點
作
交
于點
，且
，過點
作
，交
于點
，連接
，設
.
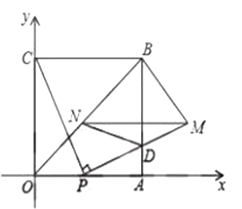
（1）求點
的坐標（用含
的代數式表示）
（2）試判斷線段
的長度是否隨點
的位置的變化而改變？并說明理由.
（3）當
為何值時，四邊形
的面積最小.
（4）在
軸正半軸上存在點
，使得
是等腰三角形，請直接寫出不少于4個符合條件的點
的坐標（用含
的式子表示）
【答案】（1）
（2）
的長度不變（3）
（4）
， 
， 
【解析】【試題分析】（1）作
于點
，依據
，及
，推得
，即
，進而依據
，推得
，借助
，推出
≌
（
），求出
， 
，則
進而求出點
的坐標為
；（2）借助
，點
，求出直線
的解析式為： 
，然后再依據點
在直線
上，且
，求得
，進而得到點
，從而求出
，即
的長度不變；（3）借助（1）的結論
，及
，推得
∽
，故
，從而求得
， 
， 
，建立函數
，求出當
時，四邊形
的面積最小，最小值6；（4）借助圖形的直觀可以探求出在
軸正半軸上存在點
，使得
是等腰三角形，此時點
的坐標為： 
， 
， 
， 
：
解：（1）作
于點
，∴
，
∵
，∴
，∴
，
又∵
，∴
，∵
，
∴
≌
（
）
∴
， 
，∴
∴點
的坐標為
.
（2）線段
長度不變.
∵
，點
，∴直線
的解析式為： 
，
∵點
在直線
上，且
， 
，∴點
∴
，即
的長度不變.
（3）由（1）知， 
，又∵
∴
∽
，∴
，
∵
， 
，∴
∴
，得
，
∴
∵
， 
， 
∴
∴當
時，四邊形
的面積最小，最小值6；
（4）在
軸正半軸上存在點
，使得
是等腰三角形，此時點
的坐標為： 
， 
， 
， 
金版課堂課時訓練系列答案
單元全能練考卷系列答案
新黃岡兵法密卷系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓
＝1(a>b>0)的離心率e＝
，連結橢圓的四個頂點得到的菱形的面積為4.
(1)求橢圓的方程；
(2)設直線l與橢圓相交于不同的兩點A，B.已知點A的坐標為(－a，0)．若|AB|＝
，求直線l的傾斜角．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分14分）
已知函數
（
為常數）的圖像與
軸交于點
，曲線
在點
處的切線斜率為
.
（1）求
的值及函數
的極值；
（2）證明：當
時，
（3）證明：對任意給定的正數
，總存在
，使得當
時，恒有
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】用0，1，2， 3，4，5這六個數字：
（1）能組成多少個無重復數字的四位偶數？
（2）能組成多少個無重復數字且為5的倍數的五位數？
（3）能組成多少個無重復數字且比1325大的四位數？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于函數f(x)，若存在x0∈R，使得f(x0)=x0成立，則稱x0為f(x)的天宮一號點.已知函數f(x)=ax2+(b-7)x+18的兩個天宮一號點分別是-3和2.
(1)求a,b的值及f(x)的表達式；
(2)當函數f(x)的定義域是［t,t+1］時，求函數f(x)的最大值g(t).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
