
【題目】若數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,則下列命題:(1)若數(shù)列
,則下列命題:(1)若數(shù)列![]() 是遞增數(shù)列,則數(shù)列
是遞增數(shù)列,則數(shù)列![]() 也是遞增數(shù)列;(2)數(shù)列
也是遞增數(shù)列;(2)數(shù)列![]() 是遞增數(shù)列的充要條件是數(shù)列
是遞增數(shù)列的充要條件是數(shù)列![]() 的各項均為正數(shù);(3)若
的各項均為正數(shù);(3)若![]() 是等差數(shù)列(公差
是等差數(shù)列(公差![]() ),則
),則![]() 的充要條件是
的充要條件是![]() ;(4)若
;(4)若![]() 是等比數(shù)列,則
是等比數(shù)列,則![]() 的充要條件是
的充要條件是![]() .其中,正確命題的個數(shù)是( )
.其中,正確命題的個數(shù)是( )
A. 0個B. 1個C. 2個D. 3個
【答案】B
【解析】
利用等差數(shù)列、等比數(shù)列的定義和性質(zhì),數(shù)列的前n項和的意義,通過舉反例可得(1)、(2)、(3)不正確.經(jīng)過檢驗,只有(4)正確,從而得出結(jié)論.
解:數(shù)列{an}的前n項和為Sn,故 Sn=a1+a2+a3+…+an,
若數(shù)列{an}是遞增數(shù)列,則數(shù)列{Sn}不一定是遞增數(shù)列,如當an<0 時,數(shù)列{Sn}是遞減數(shù)列,故(1)不正確.
由數(shù)列{Sn}是遞增數(shù)列,不能推出數(shù)列{an}的各項均為正數(shù),如數(shù)列:0,1,2,3,…,
滿足{Sn}是遞增數(shù)列,但不滿足數(shù)列{an}的各項均為正數(shù),故(2)不正確.
若{an}是等差數(shù)列(公差d≠0),則由S1S2…Sk=0不能推出a1a2…ak=0,例如數(shù)列:﹣3,﹣1,1,3,
滿足S4=0,但 a1a2a3a4≠0,故(3)不正確.
若{an}是等比數(shù)列,則由S1S2…Sk=0(k≥2,k∈N)可得數(shù)列的{an}公比為﹣1,故有an+an+1=0.
由an+an+1=0可得數(shù)列的{an}公比為﹣1,可得S1S2…Sk=0(k≥2,k∈N),故(4)正確.
故選:B.


科目:高中數(shù)學 來源: 題型:
【題目】已知直三棱柱ABC﹣A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,則異面直線AB1與BC1所成角的余弦值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在四棱錐P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,![]() ,
,![]() ,
,
以AC的中點O為球心,AC為直徑的球面交PD于點M,交PC于點N.

(1)求證:平面ABM⊥平面PCD;
(2)求直線CD與平面ACM所成角的大小;
(3)求點N到平面ACM的距離.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若![]() ,
,
(Ⅰ)求證:![]() ;
;
(Ⅱ)求證:![]() ;
;
(Ⅲ)在(Ⅱ)中的不等式中,能否找到一個代數(shù)式,滿足![]() 所求式
所求式![]() ?若能,請直接寫出該代數(shù)式;若不能,請說明理由.
?若能,請直接寫出該代數(shù)式;若不能,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】空氣質(zhì)量指數(shù)AQI是反映空氣質(zhì)量狀況的指數(shù),AQI指數(shù)值越小,表明空氣質(zhì)量越好,其對應(yīng)關(guān)系如下表:
AQI指數(shù)值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空氣質(zhì)量 | 優(yōu) | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
下圖是某市10月1日—20日AQI指數(shù)變化趨勢:

下列敘述錯誤的是
A. 這20天中AQI指數(shù)值的中位數(shù)略高于100
B. 這20天中的中度污染及以上的天數(shù)占![]()
C. 該市10月的前半個月的空氣質(zhì)量越來越好
D. 總體來說,該市10月上旬的空氣質(zhì)量比中旬的空氣質(zhì)量好
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
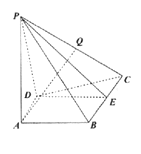
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,在直角梯形
,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 為線段
為線段![]() 的中點
的中點
(1)求證:平面![]() 平面
平面![]()
(2)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出點
?若存在,求出點![]() 的位置;若不存在,請說明理由
的位置;若不存在,請說明理由
(3)若![]() 是
是![]() 中點,
中點,![]() ,
,![]() ,
,![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】二項式![]() 的二項式系數(shù)和為256.
的二項式系數(shù)和為256.
(1)求展開式中二項式系數(shù)最大的項;
(2)求展開式中各項的系數(shù)和;
(3)展開式中是否有有理項,若有,求系數(shù);若沒有,說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com