
已知函數
(1)求函數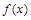 在點(0,f(0))處的切線方程;
在點(0,f(0))處的切線方程;
(2)求函數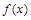 單調遞增區間;
單調遞增區間;
(3)若
 ∈[1,1],使得
∈[1,1],使得 (e是自然對數的底數),求實數
(e是自然對數的底數),求實數 的取值范圍.
的取值范圍.
(1)函數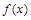 在點
在點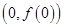 處的切線方程為
處的切線方程為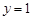 ;(2)函數
;(2)函數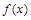 單調遞增區間
單調遞增區間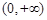 ;
;
(3)實數a的取值范圍是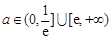 .
.
解析試題分析:⑴ 先根據函數解析式求出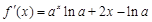 ,把
,把 代入求出斜率,進而求得切線方程;⑵ 因為當
代入求出斜率,進而求得切線方程;⑵ 因為當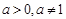 時,總有
時,總有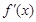 在
在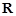 上是增函數, 又
上是增函數, 又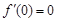 ,所以函數
,所以函數 的單調增區間為
的單調增區間為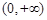 ;⑶ 要使
;⑶ 要使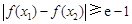 成立,只需
成立,只需 成立即可;再分
成立即可;再分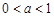 和
和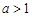 兩種情況討論即可.
兩種情況討論即可.
試題解析:⑴ 因為函數 ,
,
所以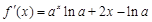 ,
,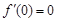 , 2分
, 2分
又因為 ,所以函數
,所以函數 在點
在點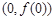 處的切線方程為
處的切線方程為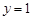 . 4分
. 4分
⑵ 由⑴,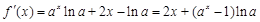 .
.
因為當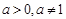 時,總有
時,總有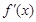 在
在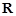 上是增函數,
上是增函數,
又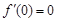 ,所以不等式
,所以不等式 的解集為
的解集為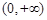 ,
,
故函數 的單調增區間為
的單調增區間為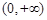 8分
8分
⑶ 因為存在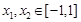 ,使得
,使得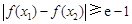 成立,
成立,
而當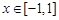 時,
時, ,
,
所以只要 即可 9分
即可 9分
又因為 ,
,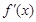 ,
, 的變化情況如下表所示:
的變化情況如下表所示: