
【題目】二次函數![]() 的圖象頂點為
的圖象頂點為![]() ,且圖象在
,且圖象在![]() 軸上截得的線段長為8.
軸上截得的線段長為8.
(1)求函數![]() 的解析式;
的解析式;
(2)令![]() .
.
(ⅰ)求函數![]() 在
在![]() 上的最小值;
上的最小值;
(ⅱ)若![]() 時,不等式
時,不等式![]() 恒成立,試求實數
恒成立,試求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)(i)分類討論,詳見解析;(ii)
;(2)(i)分類討論,詳見解析;(ii)![]() .
.
【解析】
(1)先設二次函數![]() 為頂點式,然后根據其頂點為
為頂點式,然后根據其頂點為![]() ,可知函數
,可知函數![]() 的解析式為
的解析式為![]() ,由圖象在
,由圖象在![]() 軸上截得的線段長為8,利用韋達定理即可解.
軸上截得的線段長為8,利用韋達定理即可解.
(2)(i)先求出函數![]() 的解析式,再根據
的解析式,再根據![]() ,分類討論函數
,分類討論函數![]() 的對稱軸
的對稱軸![]() ,當
,當![]() 時,函數
時,函數![]() 最小值的情況.
最小值的情況.
(ii)不等式![]() 恒成立轉化為函數
恒成立轉化為函數![]() 在區間
在區間![]() 上最大值小于等于17,再利用分類討論思想討論a的范圍即可解.
上最大值小于等于17,再利用分類討論思想討論a的范圍即可解.
解:(1)由題意設![]() ,與
,與![]() 軸的交點坐標為
軸的交點坐標為![]() ,
,![]()
∴![]() ,∵
,∵![]() ,
,
由韋達定理可得![]() .
.
∴![]() ,
,
∴![]() ,∴
,∴![]()
(2)![]() ,
,
對稱軸為![]() ,
,
(ⅰ)當![]() 時,函數
時,函數![]() 在區間
在區間![]() 為單調減函數,
為單調減函數,
∴![]() ;
;
當![]() 時,函數
時,函數![]() 在區間
在區間![]() 上為單調增函數,在區間
上為單調增函數,在區間![]() 上為單調減函數,
上為單調減函數,
![]() .
.
當![]() 時,函數
時,函數![]() 在區間
在區間![]() 上為單調增函數,
上為單調增函數,
在區間![]() 上為單調減函數,∴
上為單調減函數,∴![]() .
.
當![]() 時,
時,![]() .
.
∴函數![]() 在
在![]() 上的最小值為
上的最小值為![]() .
.
(ⅱ)①當![]() 時,
時,![]() 恒成立,只需
恒成立,只需![]() ,即
,即![]() ,顯然成立,∴
,顯然成立,∴![]() .
.
②當![]() 時,
時,![]() 恒成立,只需
恒成立,只需![]() ,即
,即![]() ,
,
即![]() ,∴
,∴![]() .
.
③當![]() 時,
時,![]() 恒成立,只需
恒成立,只需![]() ,即
,即![]() ,
,
即![]() ,這與
,這與![]() 矛盾,故舍去.
矛盾,故舍去.
綜上所述,![]() 的取值范圍是
的取值范圍是![]()


 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:高中數學 來源: 題型:
【題目】設a,b,c表示三條不同的直線,M表示平面,給出下列四個命題:其中正確命題的個數有( )
①若a//M,b//M,則a//b;
②若bM,a//b,則a//M;
③若a⊥c,b⊥c,則a//b;
④若a//c,b//c,則a//b.
A.0個B.1個C.2個D.3個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我們正處于一個大數據飛速發展的時代,對于大數據人才的需求也越來越大,其崗位大致可分為四類:數據開發、數據分析、數據挖掘、數據產品.以北京為例,2018年這幾類工作崗位的薪資(單位:萬元/月)情況如下表所示.
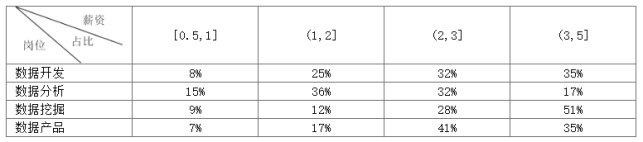
由表中數據可得各類崗位的薪資水平高低情況為
A. 數據挖掘>數據開發>數據產品>數據分析B. 數據挖掘>數據產品>數據開發>數據分析
C. 數據挖掘>數據開發>數據分析>數據產品D. 數據挖掘>數據產品>數據分析>數據開發
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com