
���}Ŀ���E�A![]() ���ҽ��c(di��n)��
���ҽ��c(di��n)��![]() ��
��![]() ��б�ʞ�
��б�ʞ�![]() ���ң�
���ң�![]() �����c(di��n)��
�����c(di��n)��![]() ��
��![]() �Ĵ�ֱƽ�־����E�A��
�Ĵ�ֱƽ�־����E�A��![]() ��
��![]() ���c(di��n)��
���c(di��n)��![]() �����c(di��n)��
�����c(di��n)��![]() .��(d��ng)
.��(d��ng)![]() �r��ֱ��
�r��ֱ��![]() ��б�ʞ�
��б�ʞ�![]() ��
��![]() ������(bi��o)ԭ�c(di��n)��.
������(bi��o)ԭ�c(di��n)��.
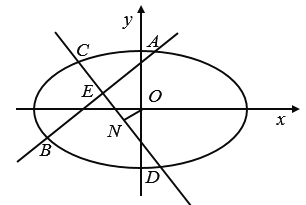
��1����E�A�Ę�(bi��o)��(zh��n)���̣�
��2���O(sh��)ԭ�c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x��
�ľ��x��![]() ����
����![]() ��ȡֵ������
��ȡֵ������
��3����ֱ��![]() ��ֱ��
��ֱ��![]() ��б�ʝM��
��б�ʝM��![]() ���Дಢ�C��
���Дಢ�C��![]() �Ƿ�鶨ֵ.
�Ƿ�鶨ֵ.
���𰸡���1��![]() ����2��
����2��![]() ����3���Ƕ�ֵ���C���^��Ҋ����.
����3���Ƕ�ֵ���C���^��Ҋ����.
��������
��1�����O(sh��)![]() ��
��![]() ������(j��)�}�⣬�õ�
������(j��)�}�⣬�õ�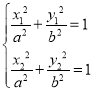 ����ʽ�������(j��)�����c(di��n)������(bi��o)�����}�⣬���
����ʽ�������(j��)�����c(di��n)������(bi��o)�����}�⣬���![]() ���ٸ���(j��)���c(di��n)����(bi��o)���õ�
���ٸ���(j��)���c(di��n)����(bi��o)���õ�![]() ����ʽ(li��n)������������Y(ji��)����
����ʽ(li��n)������������Y(ji��)����
��2�����O(sh��)ֱ��![]() �ķ��̞飺
�ķ��̞飺![]() ���c�E�A����(li��n)�����O(sh��)
���c�E�A����(li��n)�����O(sh��)![]() ��
��![]() ��
��
����(j��)�f�_(d��)���������![]() ���õ�
���õ�![]() �ķ��̞飺
�ķ��̞飺![]() ���c�E�A����(li��n)�����O(sh��)
���c�E�A����(li��n)�����O(sh��)![]() ��
��![]() ��
��
���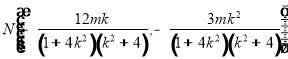 ����ʾ��
����ʾ��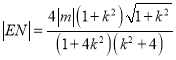 ������(j��)�c(di��n)��ֱ�����x��ʽ����ʾ��
������(j��)�c(di��n)��ֱ�����x��ʽ����ʾ��![]() ���M(j��n)���ɸ���(j��)�QԪ����ȡֵ������
���M(j��n)���ɸ���(j��)�QԪ����ȡֵ������
��3������(j��)��2���ĽY(ji��)������![]() �����
�����![]() ���������L��ʽ���քe���
���������L��ʽ���քe���![]() �c
�c![]() ���M(j��n)���ɵó��Y(ji��)��.
���M(j��n)���ɵó��Y(ji��)��.
��1���O(sh��)![]() ��
��![]() ��
��
���}�⣬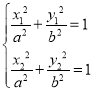 ����ʽ�����
����ʽ�����![]() ��
��
�����ã�![]() ��
��
��![]() ��б�ʞ�
��б�ʞ�![]() ���ң�
���ң�![]() �����c(di��n)��
�����c(di��n)��![]() ����(d��ng)
����(d��ng)![]() �r��ֱ��
�r��ֱ��![]() ��б�ʞ�
��б�ʞ�![]() ��
��
����![]() ����
����![]() ����
����![]() �٣�
�٣�
�֙E�A�ҽ��c(di��n)��![]() ������
������![]() �ڣ�
�ڣ�
�ɢ٢ڽ�ã�![]() ��
��![]() ��
��
��ˣ��E�A�Ę�(bi��o)��(zh��n)���̞�![]() ��
��
��2���O(sh��)ֱ��![]() �ķ��̞飺
�ķ��̞飺![]() ��
��
�� ��ȥ
��ȥ![]() �ã�
�ã�![]() ��
��
�O(sh��)![]() ��
��![]() ��
��
�t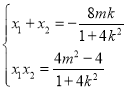 ������
������![]() ��
��
��![]() ��
��
��?y��n)?/span>![]() ��
��![]() �Ĵ�ֱƽ�־�������
�Ĵ�ֱƽ�־�������![]() �ķ��̞飺
�ķ��̞飺![]() ��
��
��![]() ��
��
��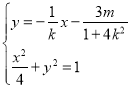 ��ȥ
��ȥ![]() �ã�
�ã�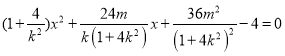 ��
��
�O(sh��)![]() ��
��![]() ��
��
�t![]() ��
��
����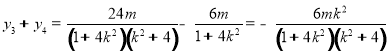 ��
��
��![]() �����c(di��n)
�����c(di��n)![]() ������(bi��o)��
������(bi��o)��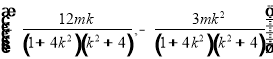 ��
��
���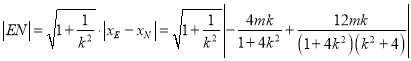
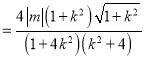 ��
��
��ԭ�c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x
�ľ��x![]() ��
��
����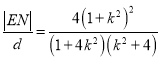 ��
��
��![]() ���t
���t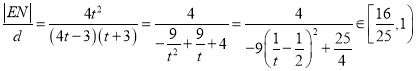 ��
��
��3���ɣ�2���ɵã�![]() ��
��
����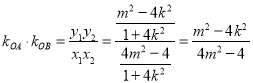 ��
��
��?y��n)�ֱ��![]() ��ֱ��
��ֱ��![]() ��б�ʝM��
��б�ʝM��![]() ��
��
����![]() �������ã�
�������ã�![]() ������
������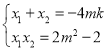 ��
��
����![]() ��
��
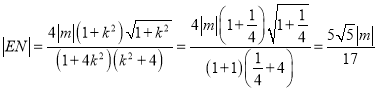 ��
��
���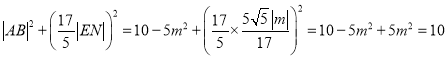 .
.
��![]() ȡ��ֵ
ȡ��ֵ![]() .
.



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ������
������![]() ����Ȼ����(sh��)�ĵה�(sh��).
����Ȼ����(sh��)�ĵה�(sh��).
��1��������(sh��)![]() �څ^(q��)�g
�څ^(q��)�g![]() ���dž��{(di��o)����(sh��)��ԇ��
���dž��{(di��o)����(sh��)��ԇ��![]() ��ȡֵ������
��ȡֵ������
��2��������(sh��)![]() �څ^(q��)�g
�څ^(q��)�g![]() ��ǡ��3�����c(di��n)����
��ǡ��3�����c(di��n)����![]() ����
����![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�AE��![]() ��ֱ��l���^ԭ�c(di��n)O�Ҳ�ƽ��������(bi��o)�S��l�cE�Ѓɂ����c(di��n)A��B������AB�����c(di��n)��M��
��ֱ��l���^ԭ�c(di��n)O�Ҳ�ƽ��������(bi��o)�S��l�cE�Ѓɂ����c(di��n)A��B������AB�����c(di��n)��M��
![]() ��
��![]() ���c(di��n)K�ڙE�AE�ϣ�
���c(di��n)K�ڙE�AE�ϣ�![]() ��
��![]() �քe��E�A�ăɂ����c(di��n)����
�քe��E�A�ăɂ����c(di��n)����![]() �ķ�����
�ķ�����
![]() �C����ֱ��OM��б���cl��б�ʵij˷e�鶨ֵ��
�C����ֱ��OM��б���cl��б�ʵij˷e�鶨ֵ��
![]() ��l�^�c(di��n)
��l�^�c(di��n)![]() ���侀OM�c�E�AE�����c(di��n)P����߅��OAPB�ܷ��ƽ����߅�Σ����ܣ���˕rֱ��lб�ʣ������ܣ��f�����ɣ�
���侀OM�c�E�AE�����c(di��n)P����߅��OAPB�ܷ��ƽ����߅�Σ����ܣ���˕rֱ��lб�ʣ������ܣ��f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����֪�����F![]() ��ӛ�����
��ӛ�����![]() ��ƽ��Ǟ�
��ƽ��Ǟ�![]() ��ֱ��
��ֱ��![]() �cƽ��
�cƽ��![]() ���ɵĽǞ�
���ɵĽǞ�![]() ��ֱ��
��ֱ��![]() �c
�c![]() ���ɵĽǞ�
���ɵĽǞ�![]() ���t�� ��
���t�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ȫ�濹���¹ڷ��������@һ����r�ڣ����н����������ͣ�n��ͣ�W(xu��)���Ŀ�̖���Ą�W(xu��)�����όW(xu��)��(x��).ijУ��(sh��)�W(xu��)�̎������{(di��o)������W(xu��)����(sh��)�W(xu��)�ɿ��c���όW(xu��)��(x��)�r�g֮�g�����P(gu��n)�P(gu��n)ϵ���������꼉�S�C(j��)�xȡ45���W(xu��)���M(j��n)�и�ۙ����������ÿ�ܾ��όW(xu��)��(x��)��(sh��)�W(xu��)�r�g������5С�r����19�ˣ����µ����У��ڙz�y��ԇ�Д�(sh��)�W(xu��)ƽ���ɿ�����120�ֵ�ռ![]() ���y(t��ng)Ӌ(j��)�ɿ���õ�����
���y(t��ng)Ӌ(j��)�ɿ���õ�����![]() ��(li��n)����
��(li��n)����
��?j��n)?sh��)������120�� | ��?j��n)?sh��)����120�� | ��Ӌ(j��) | |
���όW(xu��)��(x��)�r�g������5С�r | 4 | 19 | |
���όW(xu��)��(x��)�r�g����5С�r | |||
��Ӌ(j��) | 45 |
��1��Ո�������![]() ��(li��n)�������Д��Ƿ���99%�İ����J(r��n)���������W(xu��)���Ĕ�(sh��)�W(xu��)�ɿ��c�W(xu��)�����όW(xu��)��(x��)�r�g���P(gu��n)����
��(li��n)�������Д��Ƿ���99%�İ����J(r��n)���������W(xu��)���Ĕ�(sh��)�W(xu��)�ɿ��c�W(xu��)�����όW(xu��)��(x��)�r�g���P(gu��n)����
��2���������ӱ��Џķ�?j��n)?sh��)������120�ֵČW(xu��)���У����շӳ�ӵķ������鵽���όW(xu��)��(x��)�r�g������5С�r�;��όW(xu��)��(x��)�r�g����5С�r�ČW(xu��)����5���������@5���W(xu��)�����S�C(j��)��ȡ2�ˣ�������1��ÿ�ܾ��όW(xu��)��(x��)�r�g����5С�r�ĸ���.
��������R��ֵ����������
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
��������ʽ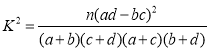 ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ʾ����֪![]() �ǙE�A
�ǙE�A![]() ��
��![]()
![]() ���ҽ��c(di��n)��ֱ��
���ҽ��c(di��n)��ֱ��![]() ��
��![]() �c�E�A
�c�E�A![]() �������c(di��n)
�������c(di��n)![]() ��
��

��1����![]() ����
����![]() ��
��
��2����![]() ��
��![]() ����E�A
����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ��
��![]() ����Ȼ����(sh��)�ĵה�(sh��)��.
����Ȼ����(sh��)�ĵה�(sh��)��.
��1��ӑՓ����(sh��)![]() �ڶ��x���(n��i)�Oֵ�c(di��n)�Ă���(sh��)��
�ڶ��x���(n��i)�Oֵ�c(di��n)�Ă���(sh��)��
��2���O(sh��)ֱ��![]() �麯��(sh��)
�麯��(sh��)![]() �ĈD����һ�c(di��n)
�ĈD����һ�c(di��n)![]() ̎���о����C�����څ^(q��)�g
̎���о����C�����څ^(q��)�g![]() �ϴ���Ψһ��
�ϴ���Ψһ��![]() ��ʹ��ֱ��
��ʹ��ֱ��![]() �c����
�c����![]() ����.
����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������Ĵ�����Ї�����(n��i)һ���B���Ї���ۡ��V�|�麣���Ї����T�Ę������̣����䳬��Ľ���Ҏ(gu��)ģ����ǰ��ʩ���y���Լ�피�Ľ��켼�g(sh��)�����磬���(n��i)��ǰ����۵��ο��ṩ�˱�ݵĽ�ͨ;����ij����������g�y(t��ng)Ӌ(j��)�˴������Ժ�����۴��?q��)��F(xi��n)��(n��i)��ǰ����۵��������ÿ͵ı����քe��![]() ���F(xi��n)ʹ�÷ӳ�ӵķ������@Щ�ÿ����S�C(j��)��ȡ
���F(xi��n)ʹ�÷ӳ�ӵķ������@Щ�ÿ����S�C(j��)��ȡ![]() �����������ÿͳ鵽60�ˣ��t�� ��
�����������ÿͳ鵽60�ˣ��t�� ��

A.�����ÿͳ鵽150��B.�����ÿͳ鵽20��
C.![]() D.���鵽�������ÿ��Լ������ÿ��˔�(sh��)֮�ͳ��^200
D.���鵽�������ÿ��Լ������ÿ��˔�(sh��)֮�ͳ��^200
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��2019��10��17�����҇���6������ؚ�ա���ij�t(y��)Ժ�_չ��ؚ�ա����t(y��)���l(xi��ng)���t(y��)���x�\��ӣ��F(xi��n)�������t(y��)�������䵽������ͬ���l(xi��ng)�(zh��n)�t(y��)Ժ�У��t(y��)���ױ�ָ�����䵽�t(y��)Ժ![]() ���t(y��)����ֻ�ܷ��䵽�t(y��)Ժ
���t(y��)����ֻ�ܷ��䵽�t(y��)Ժ![]() ���t(y��)Ժ
���t(y��)Ժ![]() ���t(y��)�������ܷ��䵽�t(y��)���ס������ڵ��t(y��)Ժ�����������t(y��)�����䵽�����t(y��)Ժ�����ԣ���ÿ���t(y��)Ժ���ٷ���һ���t(y��)�����t��ͬ�ķ��䷽������( )
���t(y��)�������ܷ��䵽�t(y��)���ס������ڵ��t(y��)Ժ�����������t(y��)�����䵽�����t(y��)Ժ�����ԣ���ÿ���t(y��)Ժ���ٷ���һ���t(y��)�����t��ͬ�ķ��䷽������( )
A.18�NB.20�NC.22�ND.24�N
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com