【答案】
分析:根據題意,用列舉法列舉全部的事件,可得其數目,
(Ⅰ)記兩數之和是3的倍數為事件A,由基本事件的列表易得事件A中含有的基本事件數目,由古典概型公式可得答案;
(Ⅱ)記“向上的兩數之積是6的倍數”為事件B,由基本事件的列表易得事件A中含有的基本事件數目,由古典概型公式可得答案;
(Ⅲ)記“點(x,y)在直線x-y=3的下方區域”為事件C,事件C的條件可以轉化為滿足x>y+3,由基本事件的列表易得事件A中含有的基本事件數目,由古典概型公式可得答案.
解答:解:根據題意,將一枚骰子先后拋擲2次,向上的點數的情況有:
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),共36種;
(Ⅰ)記兩數之和是3的倍數為事件A,則事件A中含有12個基本事件,
所以 P(A)=
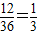
;
(Ⅱ)記“向上的兩數之積是6的倍數”為事件B,則由列表可知,事件B中含有其中的15個等可能基本事件,
所以P(B)=
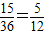
;
(Ⅲ)記“點(x,y)在直線x-y=3的下方區域”為事件C,事件C即滿足x>y+3的情況,
則由列表可知,事件C中含有其中3個基本等可能基本事件,
則P(C)=
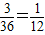
.
點評:本題考查列舉法求古典概型的概率,關鍵是用列舉法得到全部基本事件,再根據題意,查找符合條件的基本事件的數目.

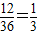 ;
;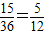 ;
;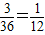 .
.
