
【題目】已知函數![]() .
.
(1)求函數![]() 的單調區間和極值;
的單調區間和極值;
(2)若![]() 有兩個零點,求實數
有兩個零點,求實數![]() 的范圍.
的范圍.
【答案】(1)增區間為![]() ,減區間為
,減區間為![]() ;極小值
;極小值![]() ,無極大值.(2)
,無極大值.(2)![]()
【解析】試題分析:(1)求出函數的導數,解關于導函數的不等式,求出函數的單調區間,進而求得函數的極值;
(2)求出函數的導數,通過討論![]() 的范圍,確定函數的單調性,求出實數
的范圍,確定函數的單調性,求出實數![]() 的范圍.
的范圍.
試題解析:(1)根據![]() ,
,
令![]() ,解得
,解得![]() ,當
,當![]() 變化時,
變化時, ![]() ,
, ![]() 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
|
|
|
| 遞減 |
| 遞增 |
∴函數![]() 的增區間為
的增區間為![]() ,減區間為
,減區間為![]() ;
;
函數![]() 在
在![]() 處取的極小值
處取的極小值![]() ,無極大值.
,無極大值.
(2)由![]() ,則
,則![]() ,
,
當![]() 時,
時, ![]() ,易知函數
,易知函數![]() 只有一個零點,不符合題意,
只有一個零點,不符合題意,
當![]() 時,在
時,在![]() 上
上![]() ,
, ![]() 單調遞減;在
單調遞減;在![]() 上
上![]() ,
, ![]() 單調遞增,又
單調遞增,又![]() ,
, ![]() ,當
,當![]() 時,
時, ![]() ,所以函數
,所以函數![]() 有兩個零點,
有兩個零點,
當![]() 時,在
時,在![]() 和
和![]() 上
上![]() ,
, ![]() 單調遞增,在
單調遞增,在![]() 上
上![]() ,
, ![]() 單調遞減.又
單調遞減.又![]()
![]() ,所以函數
,所以函數![]() 至多一個零點,不符合題意,
至多一個零點,不符合題意,
當![]() 時,在
時,在![]() 和
和![]() 上
上![]() ,
, ![]() 單調遞增,在
單調遞增,在![]() 上
上![]() ,
, ![]() 單調遞減.
單調遞減.
又![]() ,所以函數
,所以函數![]() 至多一個零點,不符合題意,
至多一個零點,不符合題意,
當![]() 時,
時, ![]() ,函數在
,函數在![]() 上單調遞增,所以函數
上單調遞增,所以函數![]() 至多一個零點,不符合題意,
至多一個零點,不符合題意,
綜上,實數![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】北京時間3月15日下午,谷歌圍棋人工智能![]() 與韓國棋手李世石進行最后一輪較量,
與韓國棋手李世石進行最后一輪較量, ![]() 獲得本場比賽勝利,最終人機大戰總比分定格
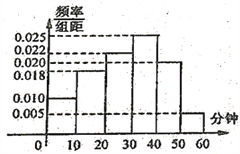
獲得本場比賽勝利,最終人機大戰總比分定格![]() .人機大戰也引發全民對圍棋的關注,某學校社團為調查學生學習圍棋的情況,隨機抽取了100名學生進行調查.根據調查結果繪制的學生日均學習圍棋時間的頻率分布直方圖(如圖所示),將日均學習圍棋時間不低于40分鐘的學生稱為“圍棋迷”.
.人機大戰也引發全民對圍棋的關注,某學校社團為調查學生學習圍棋的情況,隨機抽取了100名學生進行調查.根據調查結果繪制的學生日均學習圍棋時間的頻率分布直方圖(如圖所示),將日均學習圍棋時間不低于40分鐘的學生稱為“圍棋迷”.
(Ⅰ)根據已知條件完成下面的列聯表,并據此資料你是否有![]() 的把握認為“圍棋迷”與性別有關?
的把握認為“圍棋迷”與性別有關?
非圍棋迷 | 圍棋迷 | 合計 | |
男 | |||
女 | 10 | 55 | |
合計 |
(Ⅱ)將上述調查所得到的頻率視為概率,現在從該地區大量學生中,采用隨機抽樣方法每次抽取1名學生,抽取3次,記被抽取的3名淡定生中的“圍棋迷”人數為![]() 。若每次抽取的結果是相互獨立的,求
。若每次抽取的結果是相互獨立的,求![]() 的平均值和方差.
的平均值和方差.
附: 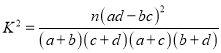 ,其中
,其中![]() .
.
| 0.05 | 0.01 |
| td style="width:124.95pt; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
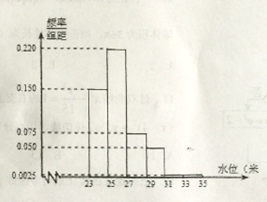
【題目】根據某水文觀測點的歷史統計數據,得到某河流水位![]() (單位:米)的頻率分布直方圖如下:將河流水位在以上6段的頻率作為相應段的概率,并假設每年河流水位互不影響.
(單位:米)的頻率分布直方圖如下:將河流水位在以上6段的頻率作為相應段的概率,并假設每年河流水位互不影響.
(Ⅰ)求未來三年,至多有1年河流水位![]() 的概率(結果用分數表示);
的概率(結果用分數表示);
(Ⅱ)該河流對沿河![]() 企業影響如下:當
企業影響如下:當![]() 時,不會造成影響;當
時,不會造成影響;當![]() 時,損失10000元;當
時,損失10000元;當![]() 時,損失60000元,為減少損失,現有三種應對方案:
時,損失60000元,為減少損失,現有三種應對方案:
方案一:防御35米的最高水位,需要工程費用3800元;
方案二:防御不超過31米的水位,需要工程費用2000元;
方案三:不采用措施:試比較哪種方案較好,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系中,已知圓![]() 的圓心坐標為
的圓心坐標為![]() ,半徑為
,半徑為![]() ,以坐標原點為極點,
,以坐標原點為極點, ![]() 軸正半軸為極軸,建立極坐標系,直線
軸正半軸為極軸,建立極坐標系,直線![]() 的參數方程為:
的參數方程為: ![]() (
(![]() 為參數)
為參數)
(1)求圓![]() 和直線
和直線![]() 的極坐標方程;
的極坐標方程;
(2)點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 與圓
與圓![]() 相較于
相較于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 經過點
經過點 ,且兩焦點與短軸的一個端點構成等腰直角三角形.
,且兩焦點與短軸的一個端點構成等腰直角三角形.
(Ⅰ)求橢圓的方程;
(Ⅱ)若圓![]() 的任意一條切線
的任意一條切線![]() 與橢圓E相交于P,Q兩點,試問:
與橢圓E相交于P,Q兩點,試問: ![]() 是否為定值? 若是,求這個定值;若不是,說明理由.
是否為定值? 若是,求這個定值;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知射手甲射擊一次,命中9環(含9環)以上的概率為0.56,命中8環的概率為0.22,命中7環的概率為0.12.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)求甲射擊一次,命中不足8環的概率;
(2)求甲射擊一次,至少命中7環的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com