
【題目】已知函數![]() ,
,![]() .
.
(![]() )設曲線
)設曲線![]() 在
在![]() 處的切線為
處的切線為![]() ,到點
,到點![]() 的距離為
的距離為![]() ,求
,求![]() 的值.
的值.
(![]() )若對于任意實數
)若對于任意實數![]() ,
,![]() 恒成立,試確定
恒成立,試確定![]() 的取值范圍.
的取值范圍.
(![]() )當
)當![]() 時,是否存在實數
時,是否存在實數![]() ,使曲線
,使曲線![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸垂直?若存在,求出
軸垂直?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(1)![]() 或
或![]() (2)
(2)![]() (3)不存在
(3)不存在
【解析】
試題
(1)該問切點橫坐標已知,則利用切點在曲線上,帶入曲線![]() 即可得到切點的縱坐標,對
即可得到切點的縱坐標,對![]() 進行求導并得到在切點處的導函數值即為切線的斜率,有切線的斜率,切線又過切點,利用直線的點斜式即可求的切線的方程,利用點到直線的距離公式結合條件點
進行求導并得到在切點處的導函數值即為切線的斜率,有切線的斜率,切線又過切點,利用直線的點斜式即可求的切線的方程,利用點到直線的距離公式結合條件點![]() 到切線的距離為
到切線的距離為![]() 即可求的參數
即可求的參數![]() 的值.
的值.
(2)該問為恒成立問題可以考慮分離參數法,即把參數a與x進行分離得到![]() ,則
,則![]() ,再利用函數的導函數研究函數
,再利用函數的導函數研究函數![]() 在區間
在區間![]() 的最大值,即可求的a的取值范圍.
的最大值,即可求的a的取值范圍.
(3)根據切線的斜率即為曲線C在切點處的導函數值,即該問可以轉化為是否存在![]() 使得
使得![]() ,令
,令![]() ,則
,則![]() 即存在
即存在![]() 使得
使得![]() ,對
,對![]() 再次求導進行最值求解可得
再次求導進行最值求解可得![]() ,所以不存在
,所以不存在![]() 使得
使得![]() .
.
試題解析:
(1)![]() ,
,![]() .
.
![]() 在
在![]() 處的切線斜率為
處的切線斜率為![]() ,
,
∴切線![]() 的方程為
的方程為![]() ,即
,即![]() . 2分
. 2分
又點![]() 到切線
到切線![]() 的距離為
的距離為![]() ,所以
,所以![]() ,
,
解之得,![]() 或
或![]() 4分
4分
(2)因為![]() 恒成立,
恒成立,
若![]() 恒成立;
恒成立;
若![]() 恒成立,即
恒成立,即![]() ,在
,在![]() 上恒成立,
上恒成立,
設![]() 則
則![]()
當![]() 時,
時,![]() ,則
,則![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() ,則
,則![]() 在
在![]() 上單調遞減;
上單調遞減;
所以當![]() 時,
時,![]() 取得最大值,
取得最大值,![]() ,
,
所以![]() 的取值范圍為
的取值范圍為![]() . 9分
. 9分
(3)依題意,曲線![]() 的方程為
的方程為![]() ,令
,令![]()
所以![]() ,
,
設![]() ,則
,則![]() ,當
,當![]() ,
,
故![]() 在
在![]() 上單調增函數,因此
上單調增函數,因此![]() 在
在![]() 上的最小值為
上的最小值為![]()
即![]()
又![]() 時,
時,![]()
所以![]()
曲線![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸垂直等價于方程
軸垂直等價于方程![]() 有實數解,但是
有實數解,但是![]() ,
,![]() 沒有實數解,故不存在實數
沒有實數解,故不存在實數![]() 使曲線
使曲線![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸垂直. 14分
軸垂直. 14分


 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:高中數學 來源: 題型:
【題目】設直線l:![]() ,圓C:
,圓C:![]() ,則下列說法中正確的是( )
,則下列說法中正確的是( )
A.直線l與圓C有可能無公共點
B.若直線l的一個方向向量為![]() ,則
,則![]()
C.若直線l平分圓C的周長,則![]()
D.若直線l與圓C有兩個不同交點M、N,則線段MN的長的最小值為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠使用兩種零件![]() 、
、![]() 裝配兩種產品
裝配兩種產品![]() 、
、![]() ,該廠的生產能力是月產
,該廠的生產能力是月產![]() 產品最多有2500件,月產
產品最多有2500件,月產![]() 產品最多有1200件;而且組裝一件
產品最多有1200件;而且組裝一件![]() 產品要4個
產品要4個![]() 、2個
、2個![]() ,組裝一件
,組裝一件![]() 產品要6個
產品要6個![]() 、8個
、8個![]() ,該廠在某個月能用的
,該廠在某個月能用的![]() 零件最多14000個;
零件最多14000個;![]() 零件最多12000個.已知
零件最多12000個.已知![]() 產品每件利潤1000元,
產品每件利潤1000元,![]() 產品每件2000元,欲使月利潤最大,需要組裝
產品每件2000元,欲使月利潤最大,需要組裝![]() 、
、![]() 產品各多少件?最大利潤多少萬元?
產品各多少件?最大利潤多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面給出四種說法:
①設![]() 、
、![]() 、
、![]() 分別表示數據
分別表示數據![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的平均數、中位數、眾數,則
的平均數、中位數、眾數,則![]() ;
;
②在線性回歸模型中,相關指數![]() 表示解釋變量對于預報變量變化的貢獻率,
表示解釋變量對于預報變量變化的貢獻率,![]() 越接近于
越接近于![]() ,表示回歸的效果越好;
,表示回歸的效果越好;
③繪制頻率分布直方圖時,各小長方形的面積等于相應各組的組距;
④設隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() .
.
其中不正確的是( ).
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為確定下一年度投入某種產品的宣傳費,需了解年宣傳費![]() (單位:千元)對年銷售量
(單位:千元)對年銷售量![]() (單位:
(單位: ![]() )和年利潤
)和年利潤![]() (單位:千元)的影響,對近8年的年宣傳費
(單位:千元)的影響,對近8年的年宣傳費![]() 和年銷售量
和年銷售量![]() 數據作了初步處理,得到下面的散點圖及一些統計量的值.
數據作了初步處理,得到下面的散點圖及一些統計量的值.

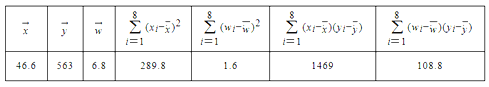
表中![]() ,
,![]() .
.
(1)根據散點圖判斷, ![]() 與
與![]() 哪一個適宜作為年銷售量
哪一個適宜作為年銷售量![]() 關于年宣傳費
關于年宣傳費![]() 的回歸方程類型?(給出判斷即可,不必說明理由)
的回歸方程類型?(給出判斷即可,不必說明理由)
(2)根據(1)的判斷結果及表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)已知這種產品的年利潤![]() 與
與![]() 、
、![]() 的關系為
的關系為![]() .根據(2)的結果要求:年宣傳費
.根據(2)的結果要求:年宣傳費![]() 為何值時,年利潤最大?
為何值時,年利潤最大?
附:對于一組數據![]() ,
, ![]() ,…,
,…, ![]() 其回歸直線
其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為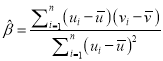 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=lg(﹣x2+5x﹣6)的定義域為A,函數g(x)![]() ,x∈(0,m)的值域為B.
,x∈(0,m)的值域為B.
(1)當m=2時,求A∩B;
(2)若“x∈A”是“x∈B”的必要不充分條件,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com