如圖,圓錐
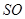
中,
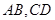
為底面圓的兩條直徑 ,AB交CD于O,且
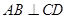
,
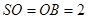
,
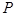
為
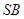
的中點.
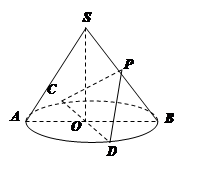
(1)求證:
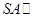
平面
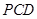
;
(2)求圓錐
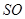
的表面積;求圓錐
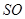
的體積。
(3)求異面直線
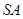
與
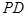
所成角的正切值 .
(1)連結(jié)

,


、

分別為
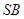
、

的中點,


,

平面

(2)表面積為

,體積為

(3)

試題分析:(1)連結(jié)

, 1分


、

分別為
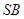
、

的中點,

, 2分

,

平面

. 4分(表述缺漏扣1分)
(2)

, 5分,

, 6分

,

8分
(3)

,

為異面直線
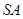
與

所成角. …9分

,

, 10分

.在

中,

,

, 11分

,

異面直線
與

所成角的正切值為

. 12分
點評:證明線面平行可證明直線與平面內(nèi)的一條直線平行,即轉(zhuǎn)化為線線平行,求異面直線所成角時首先將異面直線平移為相交直線,常通過中位線等產(chǎn)生的平行關(guān)系實現(xiàn)平移,找到所求角進而解三角形得到角的大小
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:單選題
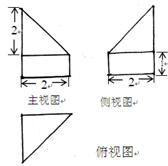
如圖為一幾何體的三視圖,則該幾何體體積為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
下圖表示一個幾何體的三視圖及相應數(shù)據(jù),則該幾何體的體積是

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若正方體的棱長為

,則以該正方體各個面的中心為頂點的凸多面體的體積為 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
一個幾何體的三視圖如右圖所示,且其左視圖是一個等邊三角形,則這個幾何體的體積為( )

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知某幾何體的三視圖如圖所示,若該幾何體的體積為24,則正視圖中a的值為

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
三棱柱三視圖(主視圖和俯視圖是正方形,左視圖是等腰直角三角形)如圖所示, 則這個三棱柱的全面積等于 ( )

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
三棱錐A-BCD的三條側(cè)棱兩兩互相垂直,且AB=2, AD=

,AC=1,則A,B兩點在三棱錐的外接球的球面上的距離為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
如圖示,AB是圓柱的母線,BD是圓柱底面圓的直徑,C是底面圓周上一點,E是AC中點,且
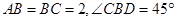
.
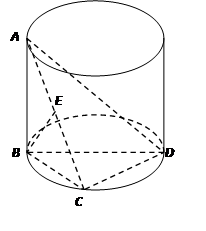
(1)求證:
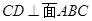
;
(2)求直線BD與面ACD所成角的大小.
查看答案和解析>>

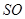 中,
中,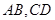 為底面圓的兩條直徑 ,AB交CD于O,且
為底面圓的兩條直徑 ,AB交CD于O,且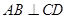 ,
,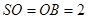 ,
,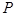 為
為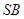 的中點.
的中點.
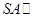 平面
平面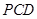 ;
;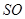 的表面積;求圓錐
的表面積;求圓錐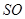 的體積。
的體積。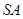 與
與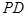 所成角的正切值 .
所成角的正切值 . ,AC=1,則A,B兩點在三棱錐的外接球的球面上的距離為( )
,AC=1,則A,B兩點在三棱錐的外接球的球面上的距離為( )



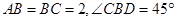 .
.
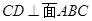 ;
;