
【題目】已知空間四邊形ABCD,E、H分別是AB、AD的中點,F、G分別是邊BC、DC的三等分點(如圖), 
求證:
(1)對角線AC、BD是異面直線;
(2)直線EF和HG必交于一點,且交點在AC上.
【答案】
(1)證明:假設對角線AC、BD在同一平面α內,
則A、B、C、D都在平面α內,這與ABCD是空間四邊形矛盾,
∴AC、BD是異面直線.
(2)證明:∵E、H分別是AB、AD的中點,∴EH BD.
又F、G分別是BC、DC的三等分點,
∴FG BD.∴EH∥FG,且EH<FG.
∴FE與GH相交.
設交點為O,又O在GH上,GH在平面ADC內,∴O在平面ADC內.
同理,O在平面ABC內.
從而O在平面ADC與平面ABC的交線AC上.
【解析】(1)利用反證法證明對角線AC、BD是共面直線,推出矛盾,從而證明是異面直;(2)說明直線EF和HG必交于一點,然后證明這點在平面ADC內.又在平面ABC內,必在它們的交線AC上.
【考點精析】認真審題,首先需要了解平面的基本性質及推論(如果一條直線上的兩點在一個平面內,那么這條直線在此平面內;過不在一條直線上的三點,有且只有一個平面;如果兩個不重合的平面有一個公共點,那么它們有且只有一條過該點的公共直線),還要掌握異面直線的判定(過平面外一點與平面內一點的直線和平面內不經過該點的直線是異面直線.(不在任何一個平面內的兩條直線))的相關知識才是答題的關鍵.


科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,底面△ABC為等腰直角三角形,∠B=90°,D為棱BB1上一點,且平面DA1C⊥平面AA1C1C. 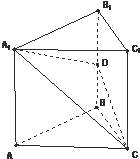
(1)求證:D點為棱BB1的中點;
(2)判斷四棱錐A1﹣B1C1CD和C﹣A1ABD的體積是否相等,并證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() .
.
(Ⅰ)當![]() 時,求函數
時,求函數![]() 的極值;
的極值;
(Ⅱ)當![]() 時,討論函數
時,討論函數![]() 單調性;
單調性;
(Ⅲ)是否存在實數![]() ,對任意的
,對任意的![]() ,
, ![]() ,且
,且![]() ,有
,有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}滿足a1+3a2+32a3+…+3n﹣1an= ![]() (n∈N*).
(n∈N*).
(1)求數列{an}的通項公式;
(2)設bn= ![]() ,求數列{bn}的前n項和Sn .
,求數列{bn}的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右兩個焦點分別為
的左、右兩個焦點分別為![]() ,離心率
,離心率![]() ,短軸長為2.
,短軸長為2.
(1)求橢圓的方程;
(2)點![]() 為橢圓上的一動點(非長軸端點),
為橢圓上的一動點(非長軸端點),![]() 的延長線與橢圓交于
的延長線與橢圓交于![]() 點,
點, ![]() 的延長線與橢圓交于
的延長線與橢圓交于![]() 點,求
點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合M={x|![]() ≤1},N={x|y=lg(1﹣x)},則下列關系中正確的是( )
≤1},N={x|y=lg(1﹣x)},則下列關系中正確的是( )
A.(RM)∩N=
B.M∪N=R
C.MN
D.(RM)∪N=R
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com