如圖,在平面直角坐標系

中,
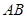
是半圓

的直徑,
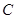
是半圓

(除端點
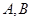
)上的任意一點.在線段

的延長線上取點

,使

,試求動點

的軌跡方程

點
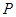
的軌跡方程為
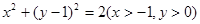
試題分析:[解法一]連結
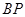
,由已知可得
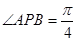
,
∴ 點
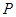
在以
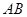
為弦,所對圓周角為
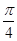
的圓上.
設該圓的圓心為
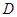
,則點
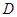
在弦
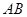
的中垂線上,即
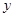
軸上,且

,
∴
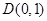
,
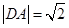
.圓
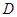
的方程為
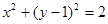
.
當點
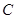
趨近于點
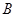
時,點
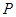
趨近于點
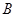
;當點
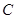
趨近于點
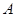
時,點
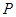
趨近于點
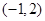
.
所以點
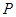
的軌跡方程為
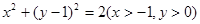
[解法二] 連結
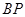
,由已知可得
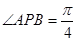
,
設
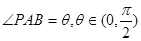
,則
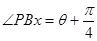
故若設直線
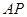
的斜率為
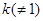
時,直線
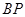
的斜率為
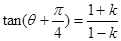
.
故
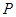
為兩直線
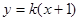
及
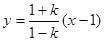
的交點,消去
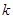
得
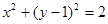
,當
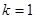
時,
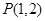
也在該圓上.
結合
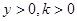
可知,點
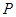
的軌跡方程為
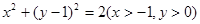
點評:解決該試題的關鍵是建立動點滿足的關系式,設出點的坐標,建立關系式,將關系式坐標化,然后化簡得到其軌跡方程,一般來說,先考慮運用定義法求解軌跡,再考慮運用直接法來求解,中檔題。
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:單選題
設拋物線的頂點在原點,準線方程為
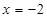
,則拋物線方程是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設橢圓的中心是坐標原點,長軸
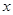
在軸上,離心率
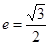
,已知點
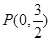
到這個橢圓上的最遠距離是
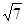
,求這個橢圓的方程.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設平面區(qū)域D是由雙曲線
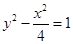
的兩條漸近線和拋物線y
2 ="-8x" 的準線所圍成的三角形(含邊界與內部).若點(x,y) ∈ D,則x+ y的最小值為
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
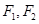
是雙曲線
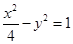
的兩個焦點,
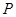
在雙曲線上且
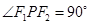
,則
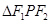
的面積為 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
曲線
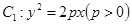
的焦點
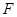
恰好是曲線

的右焦點,且曲線
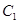
與曲線
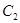
交點連線過點
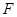
,則曲線
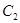
的離心率是
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
橢圓
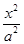
+
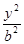
=1(a>b>0)的離心率是
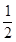
,則
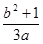
的最小值為( )
A.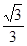 | B.1 | C.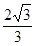 | D.2 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知橢圓的中心在原點,焦點在x軸上,焦距等于6,離心率等于
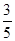
,則此橢圓的方程是
查看答案和解析>>

 中,
中,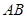 是半圓
是半圓 的直徑,
的直徑,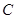 是半圓
是半圓 (除端點
(除端點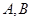 )上的任意一點.在線段
)上的任意一點.在線段 的延長線上取點
的延長線上取點 ,使
,使 ,試求動點
,試求動點 的軌跡方程
的軌跡方程
 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案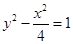 的兩條漸近線和拋物線y2 ="-8x" 的準線所圍成的三角形(含邊界與內部).若點(x,y) ∈ D,則x+ y的最小值為
的兩條漸近線和拋物線y2 ="-8x" 的準線所圍成的三角形(含邊界與內部).若點(x,y) ∈ D,則x+ y的最小值為