【題目】為了解春季晝夜溫差大小與某種子發芽多少之間的關系,現在從4月份的30天中隨機挑選了5天進行研究,且分別記錄了每天晝夜溫差與每100顆種子浸泡后的發芽數,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
溫差x/oC | 10 | 11 | 13 | 12 | 8 |
發芽數y/顆 | 23 | 25 | 30 | 26 | 16 |
(1)從這5天中任選2天,若選取的是4月1日與4月30日的兩組數據,請根據這5天中的另3天的數據,求出
關于
的線性回歸方程
(2)若由線性回歸方程得到的估計數據與所選出的兩組檢驗數據的誤差均不超過2顆,則認為得到的線性回歸方程是可靠的,試問(1)中所得的線性回歸方程是否可靠.
(參考公式,
)
【答案】（1）
；（2）見解析.
【解析】
試題分析：（1）根據表格中數據及平均數公式可求出
與
的值,從而可得樣本中心點的坐標，進而求可得公式
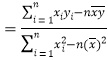中所需數據，求出
，再結合樣本中心點的性質可得
，可得
關于
的回歸方程；（2）將
分別代入所求得的回歸方程，將得到的值與實際值進行比較,看誤差是否超過
，從而可得(1)中所得的線性回歸方程是否可靠.
試題解析：(1)由已知中表格得, 4月7日, 4月15日, 4月21日這3天的數據的平均數為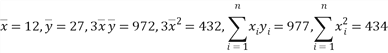
,所以
,所以y關于x的線性回歸方程為
,
(2)依題意得,當
時,
;當
時,
,所以(2)中所得的線性回歸方程是可靠的.
【方法點晴】本題主要考查線性回歸方程求法與應用，屬于中檔題.求回歸直線方程的步驟：①依據樣本數據畫出散點圖，確定兩個變量具有線性相關關系；②計算
的值；③計算回歸系數
；④寫出回歸直線方程為
； 回歸直線過樣本點中心
是一條重要性質，利用線性回歸方程可以估計總體，幫助我們分析兩個變量的變化趨勢.
科目：高中數學 來源： 題型：
【題目】如圖，在四面體A-BCD中，AD
平面BCD,BCCD,CD=2,AD=4.M是AD的中點，P是BM的中點，點Q在線段AC上，且AQ=3QC.
(I)證明：PQ//平面BCD;
(II)若異面直線PQ與CD所成的角為
，二面角C-BM-D的大小為
，求cos的值。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，長方體ABCD﹣A1B1C1D1中，AA1=AB=1，AD=2，E為BC的中點，點M，N分別為棱DD1 ， A1D1的中點．
（1）求證：平面CMN∥平面A1DE；
（2）求證：平面A1DE⊥平面A1AE．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）是定義在[﹣2，2]上的奇函數，當x∈（0，2]時，f（x）=2x﹣1，函數g（x）=x2﹣2x+m．如果對于x1∈[﹣2，2]，x2∈[﹣2，2]，使得g（x2）=f（x1），則實數m的取值范圍是
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知定義在（0， 
）上的函數f（x），f'（x）為其導數，且 
＜ 
恒成立，則（ ）
A.
f（ 
）＞ 
f（ 
）
B. f（ 
）＞f（ ）??
C.f（1）＜2f（ ）sin1
D. f（ ）＜f（ ）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
