【題目】已知函數
．
（Ⅰ）當
時，求函數 
的單調區(qū)間；
（Ⅱ）當
時，不等式
恒成立，求實數
的取值范圍．
（Ⅲ）求證： 
（
， 
是自然對數的底數）.
【答案】（Ⅰ）單調遞增區(qū)間為
，單調遞減區(qū)間為
;（Ⅱ）
; （Ⅲ）見解析.
【解析】分析：（Ⅰ）求出函數的導數，分別解不等式
、
，可求得
的增區(qū)間和減區(qū)間.
（Ⅱ）構建新函數
， 不等式
在
上恒成立等價于
在
恒成立，而
，分
三種情形討論可得實數
的取值范圍為
.
（Ⅲ）由（Ⅱ）得不等式
， 
，故有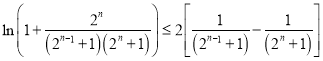
，利用累加及其裂項相消法可以得到： 
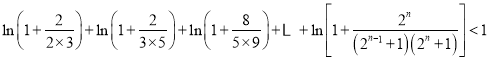，化簡后可得到要證明的不等式.
詳解：（Ⅰ）當
時， 
，
.
由
解得
，由
解得
，
故函數
的單調遞增區(qū)間為
，單調遞減區(qū)間為
（Ⅱ）因當
時，不等式
恒成立，即
恒成立.
設
，只需
即可.
由
,
（ⅰ）當
時， 
，
當
時， 
，函數
在
上單調遞減，
故
成立；
（ⅱ）當
時，由
，因
，所以
，
①若
，即
時，在區(qū)間
上， 
，則函數
在
上單調遞增， 
在
上無最大值；
②若
，即
時，函數
在
上單調遞減，在區(qū)間
上單調遞增，同樣
在
上無最大值，不滿足條件；
（ⅲ）當
時，由
，∵
，∴
，
∴
，故函數
在
上單調遞減，故
成立.
綜上所述，實數
的取值范圍是
.
（Ⅲ）據（Ⅱ）知當
時， 
在
上恒成立，又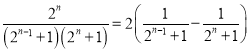
，
∵
，
∴
.
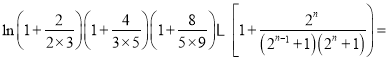
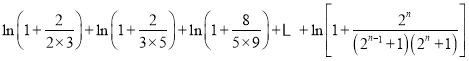
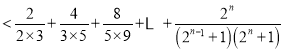
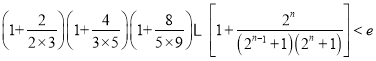閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知某種藥物在血液中以每小時
的比例衰減，現給某病人靜脈注射了該藥物2500mg，設經過x個小時后，藥物在病人血液中的量為ymg．
與x的關系式為______；
當該藥物在病人血液中的量保持在1500mg以上，才有療效；而低于500mg，病人就有危險，要使病人沒有危險，再次注射該藥物的時間不能超過______小時
精確到
．
參考數據：
，
，
，
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知在圓x2+y2﹣4x+2y=0內，過點E（1，0）的最長弦和最短弦分別是AC和BD，則四邊形ABCD的面積為（ ）
A.
B.6 
C.
D.2 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C： 
=1（a＞b＞0）的離心率為 
，且過定點M（1， ）．
（1）求橢圓C的方程；
（2）已知直線l：y=kx﹣ 
（k∈R）與橢圓C交于A、B兩點，試問在y軸上是否存在定點P，使得以弦AB為直徑的圓恒過P點？若存在，求出P點的坐標和△PAB的面積的最大值，若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】平面直角坐標系中，直線l的參數方程 
（t為參數），以坐標原點為極點，x軸的正半軸為極軸，建立極坐標系，已知曲線C的極坐標方程為p2cos2θ+p2sinθ﹣2psinθ﹣3=0
（1）求直線l的極坐標方程；
（2）若直線l與曲線C相交于A，B兩點，求|AB|．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某村莊擬修建一個無蓋的圓柱形蓄水池(不計厚度)．設該蓄水池的底面半徑為r米，高為h米，體積為V立方米．假設建造成本僅與表面積有關，側面的建造成本為100元/平方米，底面的建造成本為160元/平方米，該蓄水池的總建造成本為12 000π元(π為圓周率)．
(1)將V表示成r的函數V(r)，并求該函數的定義域；
(2)討論函數V(r)的單調性，并確定r和h為何值時該蓄水池的體積最大．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列命題中，正確的命題是
A. 任意三點確定一個平面
B. 三條平行直線最多確定一個平面
C. 不同的兩條直線均垂直于同一個平面，則這兩條直線平行
D. 一個平面中的兩條直線與另一個平面都平行，則這兩個平面平行
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給定下列四個命題：
若一個平面內的兩條直線與另一個平面都平行，那么這兩個平面相互平行；
若一個平面經過另一個平面的垂線，那么這兩個平面相互垂直；
垂直于同一直線的兩條直線相互平行；
若兩個平面垂直，那么一個平面內與它們的交線不垂直的直線與另一個平面也不垂直．
其中，為真命題的是
A. 和 B. 和 C. 和 D. 和
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
