【題目】已知函數(shù)
（
，
）,其圖像與直線
相鄰兩個交點的距離為
,若
對于任意的
恒成立, 則
的取值范圍是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
由題意可得函數(shù)的周期為
=π，求得ω=2．再根據(jù)當(dāng)x∈（﹣
，
）時，sin（2x+φ）＞0恒成立，2kπ＜2（﹣）+φ＜2+φ＜2kπ+π，由此求得φ的取值范圍．
函數(shù)f(x)=2sin(ωx+φ)+1
,其圖象與直線y=-1相鄰兩個交點的距離為π,故函數(shù)的周期為
=π,所以ω=2,于是f(x)=2sin(2x+φ)+1.
若f(x)>1對x∈
恒成立,即當(dāng)x∈時,sin(2x+φ)>0恒成立,
則有2kπ≤2·
+φ<2·+φ≤2kπ+π,求得2kπ+
≤φ≤2kπ+,k∈Z,又|φ|≤
,所以≤φ≤.
故答案為：D
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，已知四邊形ABCD和BCEG均為直角梯形，AD∥BC，CE∥BG，且∠BCD=∠BCE= 
，平面ABCD⊥平面BCEG，BC=CD=CE=2BG=2． 
（1）證明：AG∥平面BDE；
（2）求二面角E﹣BD﹣G的余弦值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
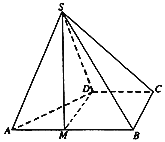
【題目】四棱錐S－ABCD的底面ABCD為直角梯形，AB∥CD，AB⊥BC，AB＝2BC＝2CD＝2，△SAD為正三角形．
（Ⅰ）點M為棱AB上一點，若BC∥平面SDM，AM＝λAB，求實數(shù)λ的值；
（Ⅱ）若BC⊥SD，求二面角A－SB－C的余弦值．
【答案】（Ⅰ）
（Ⅱ）
【解析】
（Ⅰ）由線面平行的性質(zhì)定理可得
，據(jù)此可知四邊形BCDM為平行四邊形，據(jù)此可得.
（Ⅱ）由幾何關(guān)系，在平面
內(nèi)過點
作
直線
于點
，以點E為坐標(biāo)原點，EA方向為X軸，EC方向為Y軸，ES方向為Z軸建立空間坐標(biāo)系，據(jù)此可得平面
的一個法向量
，平面
的一個法向量
，據(jù)此計算可得二面角
余弦值為
.
（Ⅰ）因為
平面SDM,
平面ABCD,平面SDM 
平面ABCD=DM,所以，
因為
,所以四邊形BCDM為平行四邊形，又
,所以M為AB的中點.
因為
.
（Ⅱ）因為
， ，所以平面，又因為
平面
，
所以平面
平面，平面
平面
，
在平面內(nèi)過點作直線于點，則平面，
在
和
中，因為
，所以
，
又由題知
，所以
所以
，
以下建系求解.以點E為坐標(biāo)原點，EA方向為X軸，EC方向為Y軸，ES方向為Z軸建立如圖所示空間坐標(biāo)系，
則
，
，
，
，
，
，
，
，
，
設(shè)平面的法向量
，則
，所
，
令
得為平面的一個法向量，
同理得為平面的一個法向量，
，因為二面角為鈍角.
所以二面角余弦值為.
【點睛】
本題考查了立體幾何中的判斷定理和二面角的求解問題，意在考查學(xué)生的空間想象能力和邏輯推理能力；解答本題關(guān)鍵在于能利用直線與直線、直線與平面、平面與平面關(guān)系的相互轉(zhuǎn)化，通過嚴(yán)密推理，明確角的構(gòu)成.同時對于立體幾何中角的計算問題，往往可以利用空間向量法，通過求解平面的法向量，利用向量的夾角公式求解.
【題型】解答題
【結(jié)束】
19
【題目】小明在石家莊市某物流派送公司找到了一份派送員的工作，該公司給出了兩種日薪薪酬方案．甲方案：底薪100元，每派送一單獎勵1元；乙方案：底薪140元，每日前55單沒有獎勵，超過55單的部分每單獎勵12元．
（Ⅰ）請分別求出甲、乙兩種薪酬方案中日薪y（單位：元）與送貨單數(shù)n的函數(shù)關(guān)系式；
（Ⅱ）根據(jù)該公司所有派送員100天的派送記錄，發(fā)現(xiàn)派送員的日平均派送單數(shù)滿足以下條件：在這100天中的派送量指標(biāo)滿足如圖所示的直方圖，其中當(dāng)某天的派送量指標(biāo)在（
，
]（n＝1，2，3，4，5）時，日平均派送量為50＋2n單．若將頻率視為概率，回答下列問題：
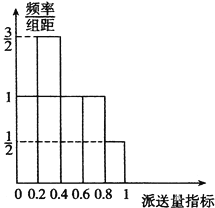
①根據(jù)以上數(shù)據(jù)，設(shè)每名派送員的日薪為X（單位：元），試分別求出甲、乙兩種方案的日薪X的分布列，數(shù)學(xué)期望及方差；
②結(jié)合①中的數(shù)據(jù)，根據(jù)統(tǒng)計學(xué)的思想，幫助小明分析，他選擇哪種薪酬方案比較合適，并說明你的理由。
（參考數(shù)據(jù)：0．62＝0．36，1．42＝1．9 6，2．6 2＝6．76，3．42＝1 1．56，3．62＝12．96，4．62＝21．16，15．62＝243．36，20．42＝416．16，44．42＝1971．36）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知某路段最高限速60km/h，電子監(jiān)控測得連續(xù)6輛汽車的速度用莖葉圖表示如下（單位：km/h）．若從中任取2輛，則恰好有1輛汽車超速的概率為（ ） 
A.
B.
C.
D.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下表是某廠生產(chǎn)某種產(chǎn)品的過程中記錄的幾組數(shù)據(jù)，其中
表示產(chǎn)量（單位：噸），
表示生產(chǎn)中消耗的煤的數(shù)量（單位：噸）.
|
|
|
|
|
|
|
|
|
|
|
|
（1）試在給出的坐標(biāo)系下作出散點圖，根據(jù)散點圖判斷，在
與
中，哪一個方程更適合作為變量關(guān)于的回歸方程模型？（給出判斷即可，不需要說明理由）
（2）根據(jù)（1）的結(jié)果以及表中數(shù)據(jù)，建立變量關(guān)于的回歸方程.并估計生產(chǎn)
噸產(chǎn)品需要準(zhǔn)備多少噸煤.參考公式：
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某房地產(chǎn)開發(fā)商為吸引更多消費(fèi)者購房,決定在一塊閑置的扇形空地中修建一個花園.如圖,已知扇形AOB的圓心角∠AOB=
,半徑為R.現(xiàn)欲修建的花園為OMNH,其中M,H分別在OA,OB上,N在
上.設(shè)∠MON=θ,OMNH的面積為S.
(1)將S表示為關(guān)于θ的函數(shù);
(2)求S的最大值及相應(yīng)的θ值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)f（x）=|x﹣a|+|x+2|．
（1）當(dāng)a=1 時，求不等式f（x）≤5的解集；
（2）x0∈R，f（x0）≤|2a+1|，求a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
.
(1)判斷函數(shù)
的單調(diào)性；
(2)若
,當(dāng)
時,不等式
恒成立,求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某商場銷售某種品牌的空調(diào)器，每周周初購進(jìn)一定數(shù)量的空調(diào)器，商場每銷售一臺空調(diào)器可獲利500元，若供大于求，則每臺多余的空調(diào)器需交保管費(fèi)100元；若供不應(yīng)求，則可從其他商店調(diào)劑供應(yīng)，此時每臺空調(diào)器僅獲利潤200元．
（Ⅰ）若該商場周初購進(jìn)20臺空調(diào)器，求當(dāng)周的利潤（單位：元）關(guān)于當(dāng)周需求量n（單位：臺，n∈N）的函數(shù)解析式f（n）；
（Ⅱ）該商場記錄了去年夏天（共10周）空調(diào)器需求量n（單位：臺），整理得表：
周需求量n | 18 | 19 | 20 | 21 | 22 |
頻數(shù) | 1 | 2 | 3 | 3 | 1 |
以10周記錄的各需求量的頻率作為各需求量發(fā)生的概率，若商場周初購進(jìn)20臺空調(diào)器，X表示當(dāng)周的利潤（單位：元），求X的分布列及數(shù)學(xué)期望．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
