
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
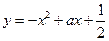 與直線
與直線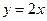
 的取值范圍;
的取值范圍; 在
在 的取值范圍內時,求拋物線截直線所得弦長的最小值。
的取值范圍內時,求拋物線截直線所得弦長的最小值。
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
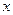 軸為對稱軸,焦點在直線
軸為對稱軸,焦點在直線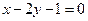 上.
上.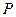 是拋物線上一點,點
是拋物線上一點,點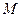 的坐標為
的坐標為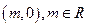 ,求
,求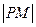 的最小值(用
的最小值(用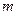 表示),并指出此時點
表示),并指出此時點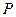 的坐標。
的坐標。查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
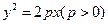 上一定點
上一定點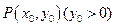 ,作兩條直線分別交拋物線于
,作兩條直線分別交拋物線于 ,(1)求該拋物線上縱坐標為
,(1)求該拋物線上縱坐標為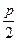 的點到其焦點
的點到其焦點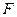 的距離;(2)當
的距離;(2)當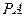 與
與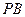 的斜率存在且傾斜角互補時,求
的斜率存在且傾斜角互補時,求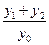 的值,并證明直線
的值,并證明直線 的斜率是非零常數(shù)。
的斜率是非零常數(shù)。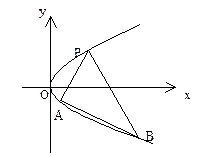
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
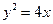 ,
,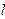 為其準線,過其對稱軸上一點P
為其準線,過其對稱軸上一點P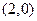 作直線
作直線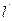 與拋物線交于A
與拋物線交于A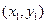 、B
、B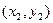 兩點,連結OA、OB并延長AO、BO分別交
兩點,連結OA、OB并延長AO、BO分別交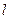 于點M、N。(1)求
于點M、N。(1)求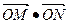 的值;
的值;
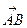 所成的比為
所成的比為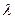 ,
,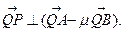 求證:
求證: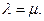
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com