
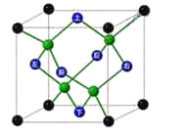
【題目】金剛石是碳原子的一種結構晶體,屬于面心立方晶胞(晶胞是構成晶體的最基本的幾何單元),即碳原子處在立方體的![]() 個頂點,
個頂點,![]() 個面的中心,此外在立方體的對角線的
個面的中心,此外在立方體的對角線的![]() 處也有
處也有![]() 個碳原子,如圖所示(綠色球),碳原子都以共價鍵結合,原子排列的基本規律是每一個碳原子的周圍都有
個碳原子,如圖所示(綠色球),碳原子都以共價鍵結合,原子排列的基本規律是每一個碳原子的周圍都有![]() 個按照正四面體分布的碳原子.設金剛石晶胞的棱長為
個按照正四面體分布的碳原子.設金剛石晶胞的棱長為![]() ,則正四面體
,則正四面體![]() 的棱長為__________;正四面體
的棱長為__________;正四面體![]() 的外接球的體積是__________.
的外接球的體積是__________.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,將其左、右焦點和短軸的兩個端點順次連接得到一個面積為
,將其左、右焦點和短軸的兩個端點順次連接得到一個面積為![]() 的正方形.
的正方形.
(1)求橢圓![]() 的方程;
的方程;
(2)直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點(均不在
兩點(均不在![]() 軸上),點
軸上),點![]() ,若直線
,若直線![]() 、
、![]() 、
、![]() 的斜率成等比數列,且
的斜率成等比數列,且![]() 的面積為
的面積為![]() (
(![]() 為坐標原點),求直線
為坐標原點),求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產某種電子產品,每件產品合格的概率均為![]() ,現工廠為提高產品聲譽,要求在交付用戶前每件產品都通過合格檢驗,已知該工廠的檢驗儀器一次最多可檢驗
,現工廠為提高產品聲譽,要求在交付用戶前每件產品都通過合格檢驗,已知該工廠的檢驗儀器一次最多可檢驗![]() 件該產品,且每件產品檢驗合格與否相互獨立.若每件產品均檢驗一次,所需檢驗費用較多,該工廠提出以下檢驗方案:將產品每
件該產品,且每件產品檢驗合格與否相互獨立.若每件產品均檢驗一次,所需檢驗費用較多,該工廠提出以下檢驗方案:將產品每![]() 個(
個(![]() )一組進行分組檢驗,如果某一組產品檢驗合格,則說明該組內產品均合格,若檢驗不合格,則說明該組內有不合格產品,再對該組內每一件產品單獨進行檢驗,如此,每一組產品只需檢驗一次或
)一組進行分組檢驗,如果某一組產品檢驗合格,則說明該組內產品均合格,若檢驗不合格,則說明該組內有不合格產品,再對該組內每一件產品單獨進行檢驗,如此,每一組產品只需檢驗一次或![]() 次.設該工廠生產
次.設該工廠生產![]() 件該產品,記每件產品的平均檢驗次數為
件該產品,記每件產品的平均檢驗次數為![]() .
.
(1)![]() 的分布列及其期望;
的分布列及其期望;
(2)(i)試說明,當![]() 越大時,該方案越合理,即所需平均檢驗次數越少;
越大時,該方案越合理,即所需平均檢驗次數越少;
(ii)當![]() 時,求使該方案最合理時
時,求使該方案最合理時![]() 的值及
的值及![]() 件該產品的平均檢驗次數.
件該產品的平均檢驗次數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是一位發燒病人的體溫記錄折線圖,下列說法不正確的是( )
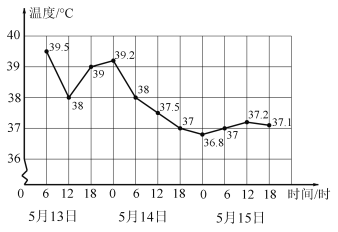
A.病人在5月13日12時的體溫是![]()
![]()
B.病人體溫在5月14日0時到6時下降最快
C.從體溫上看,這個病人的病情在逐漸好轉
D.病人體溫在5月15日18時開始逐漸穩定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數![]() 有下述四個結論:
有下述四個結論:
①函數![]() 的圖象把圓
的圖象把圓![]() 的面積兩等分
的面積兩等分
②![]() 是周期為
是周期為![]() 的函數
的函數
③函數![]() 在區間
在區間![]() 上有3個零點
上有3個零點
④函數![]() 在區間
在區間![]() 上單調遞減
上單調遞減
其中所有正確結論的編號是( )
A.①③④B.②④C.①④D.①③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在![]() 上任意一點
上任意一點![]() 處的切線
處的切線![]() 為
為![]() ,若過右焦點
,若過右焦點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,已知在點
兩點,已知在點![]() 處切線相交于
處切線相交于![]() .
.
(Ⅰ)求![]() 點的軌跡方程;
點的軌跡方程;
(Ⅱ)①若過點![]() 且與直線
且與直線![]() 垂直的直線(斜率存在且不為零)交橢圓
垂直的直線(斜率存在且不為零)交橢圓![]() 于
于![]() 兩點,證明
兩點,證明![]() 為定值.
為定值.
②四邊形![]() 的面積是否有最小值,若有請求出最小值;若沒有請說明理由.
的面積是否有最小值,若有請求出最小值;若沒有請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】廠家在產品出廠前,需對產品做檢驗,廠家將一批產品發給商家時,商家按合同規定也需隨機抽取一定數量的產品做檢驗,以決定是否接收這批產品.
(1)若廠家庫房中(視為數量足夠多)的每件產品合格的概率為 ![]() 從中任意取出 3件進行檢驗,求至少有
從中任意取出 3件進行檢驗,求至少有![]() 件是合格品的概率;
件是合格品的概率;
(2)若廠家發給商家![]() 件產品,其中有
件產品,其中有![]() 不合格,按合同規定 商家從這
不合格,按合同規定 商家從這![]() 件產品中任取
件產品中任取![]() 件,都進行檢驗,只有
件,都進行檢驗,只有![]() 件都合格時才接收這批產品,否則拒收.求該商家可能檢驗出的不合格產品的件數ξ的分布列,并求該商家拒收這批產品的概率.
件都合格時才接收這批產品,否則拒收.求該商家可能檢驗出的不合格產品的件數ξ的分布列,并求該商家拒收這批產品的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,直線![]() 將矩形紙
將矩形紙![]() 分為兩個直角梯形
分為兩個直角梯形![]() 和
和![]() ,將梯形
,將梯形![]() 沿邊
沿邊![]() 翻折,如圖2,在翻折的過程中(平面
翻折,如圖2,在翻折的過程中(平面![]() 和平面
和平面![]() 不重合),下面說法正確的是
不重合),下面說法正確的是
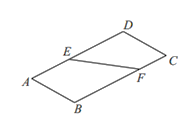
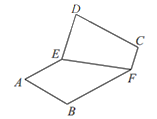
圖1 圖2
A.存在某一位置,使得![]() 平面
平面![]()
B.存在某一位置,使得![]() 平面
平面![]()
C.在翻折的過程中,![]() 平面
平面![]() 恒成立
恒成立
D.在翻折的過程中,![]() 平面
平面![]() 恒成立
恒成立
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地為鼓勵群眾參與“全民讀書活動”,增加參與讀書的趣味性.主辦方設計這樣一個小游戲:參與者拋擲一枚質地均勻的骰子(正方體,六個面上分別標注1,2,3,4,5,6六個數字).若朝上的點數為偶數.則繼續拋擲一次.若朝上的點數為奇數,則停止游戲,照這樣的規則進行,最多允許拋擲3次.每位參與者只能參加一次游戲.
(1)求游戲結束時朝上點數之和為5的概率;
(2)參與者可以選擇兩種方案:方案一:游戲結束時,若朝上的點數之和為偶數,獎勵3本不同的暢銷書;若朝上的點數之和為奇數,獎勵1本暢銷書.方案二:游戲結束時,最后一次朝上的點數為偶數,獎勵5本不同的暢銷書,否則,無獎勵.試分析哪一種方案能使游戲參與者獲得更多暢銷書獎勵?并說明判斷的理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com