
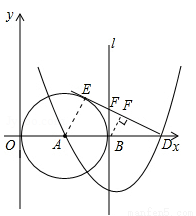
(12分)如圖,已知點A(3,0),以A為圓心作⊙A與Y軸切于原點,與x軸的另一個交點為B,過B作⊙A的切線l.

(1)以直線l為對稱軸的拋物線過點A及點C(0,9),求此拋物線的解析式;
(2)拋物線與x軸的另一個交點為D,過D作⊙A的切線DE,E為切點,求DE的長;
(3)點F是切線DE上的一個動點,當△BFD與△EAD相似時,求出BF的長 .
(1) ;(2)
;(2) ;(3)
;(3)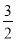 或
或 .
.
【解析】
試題分析:(1)已知了拋物線的頂點坐標,可將拋物線的解析式設為頂點坐標式,然后將C點坐標代入求解即可.
(2)由于DE是⊙A的切線,連接AE,那么根據切線的性質知AE⊥DE,在Rt△AED中,AE、AB是圓的半徑,即AE=OA=AB=3,而A、D關于拋物線的對稱軸對稱,即AB=BD=3,由此可得到AD的長,進而可利用勾股定理求得切線DE的長.
(3)若△BFD與EAD△相似,則有兩種情況需要考慮:①△AED∽△BFD,②△AED∽△FBD,根據不同的相似三角形所得不同的比例線段即可求得BF的長.
試題解析:(1)設拋物線的解析式為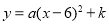 ;∵拋物線經過點A(3,0)和C(0,9),∴
;∵拋物線經過點A(3,0)和C(0,9),∴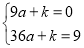 ,解得:
,解得: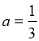 ,
,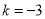 ,∴
,∴ ;
;
(2)連接AE;∵DE是⊙A的切線,∴∠AED=90°,AE=3,∵直線l是拋物線的對稱軸,點A,D是拋物線與x軸的交點,∴AB=BD=3,∴AD=6;在Rt△ADE中, =
=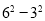 =27,∴DE=
=27,∴DE= ;
;
(3)當BF⊥ED時;∵∠AED=∠BFD=90°,∠ADE=∠BDF,∴△AED∽△BFD,∴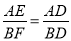 ,即
,即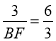 ,∴BF=
,∴BF=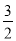 ;當FB⊥AD時,∵∠AED=∠FBD=90°,∠ADE=∠FDB,∴△AED∽△FBD,∴
;當FB⊥AD時,∵∠AED=∠FBD=90°,∠ADE=∠FDB,∴△AED∽△FBD,∴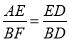 ,即BF=
,即BF=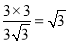 ;∴BF的長為
;∴BF的長為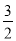 或
或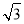 .
.
考點:二次函數綜合題.


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案科目:初中數學 來源:2014-2015學年河北省九年級上學期第二次月考數學試卷(解析版) 題型:填空題
在比例尺為1:50000的地圖上,量得甲、乙兩地的距離是3cm,則甲、乙兩地的實際距離是 m.
查看答案和解析>>
科目:初中數學 來源:2013-2014學年黑龍江省牡丹江管理局北斗星協會九年級中考三模數學試卷(解析版) 題型:選擇題
若關于x的方程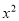 -m=2x有兩個不相等的實數根,則m的取值范圍是( )
-m=2x有兩個不相等的實數根,則m的取值范圍是( )
A.m>-1 B.m<-2 C.m≥0 D.m<0
查看答案和解析>>
科目:初中數學 來源:2013-2014學年河北省九年級上學期期末考試數學試卷(解析版) 題型:解答題
(10分)如圖,反比例函數 (
( )的圖像過等邊三角形AOB的頂點A,已知點B(-2,0).
)的圖像過等邊三角形AOB的頂點A,已知點B(-2,0).

(1)求反比例函數的表達式;
(2)若要使點B在上述反比例函數的圖像上,需將△AOB向上平移多少個單位長度?
查看答案和解析>>
科目:初中數學 來源:2013-2014學年河北省九年級上學期期末考試數學試卷(解析版) 題型:選擇題
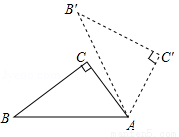
如圖,Rt△ABC中,∠C=90°,AC=3,BC=4,若以A為旋轉中心,將其按順時針方向旋轉60°到△AB'C'位置,則B點經過的路線長為( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年浙江省金華市新世紀學校七年級上學期期中數學試卷(解析版) 題型:選擇題
在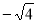 ,3.14 ,π,
,3.14 ,π,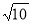 ,
,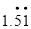 ,
,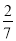 中無理數的個數是 ( )
中無理數的個數是 ( )
A.2個 B.3個 C.4個 D.5個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com