
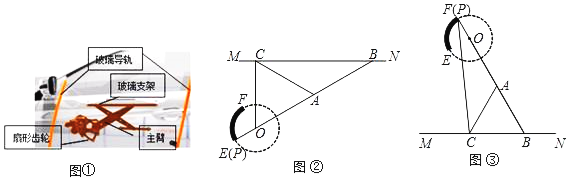
【題目】我們常見的汽車玻璃升降器如圖①所示,圖②和圖③是升降器的示意圖,其原理可以看作是主臂PB繞固定的點O旋轉,當端點P在固定的扇形齒輪![]() 上運動時,通過叉臂式結構(點B可在MN上滑動)的玻璃支架MN帶動玻璃沿導軌作上下運動而達到玻璃升降目的.點O和點P,A,B在同一直線上.當點P與點E重合時,窗戶完全閉合(圖②),此時∠ABC=30°;當點P與點F重合時,窗戶完全打開(圖③).已知
上運動時,通過叉臂式結構(點B可在MN上滑動)的玻璃支架MN帶動玻璃沿導軌作上下運動而達到玻璃升降目的.點O和點P,A,B在同一直線上.當點P與點E重合時,窗戶完全閉合(圖②),此時∠ABC=30°;當點P與點F重合時,窗戶完全打開(圖③).已知![]() 的半徑OP=5cm,
的半徑OP=5cm,![]() =
=![]() cm,OA=AB=AC=20cm.
cm,OA=AB=AC=20cm.
(1)當窗戶完全閉合時,OC=_____cm.
(2)當窗戶完全打開時,PC=_____cm.
【答案】20 5![]()
【解析】
(1)證出∠OCB=90°,△AOC是等邊三角形,由等邊三角形的性質得出OC=OA=20cm即可;
(2)連接PC,OE,作PG⊥MN于G,如圖所示:由弧長公式求出∠EOP=90°,當窗戶完全打開時,∠POC=150°,得出∠COE=150°-90°=60°,∠BOC=30°,∠ABC=60°,得出△ABC是等邊三角形,BC=OA=20,求出BP=AB+OA+OP=45,![]() ,
, ![]() ,得出CG=BG-BC=
,得出CG=BG-BC=![]() ,由勾股定理即可得出結果.
,由勾股定理即可得出結果.
解:(1)∵OA=AB=AC=20cm,
∴∠OCB=90°,
∵∠ABC=30°,
∴∠BOC=60°,
∴△AOC是等邊三角形,
∴OC=OA=20cm;
故答案為20;
(2)連接PC,OE,作PG⊥MN于G,如圖③所示:

則OCB=∠PGC=90°,
∴FG∥OC,
設∠EOP=n°,
∵![]() 的長=
的長=![]() ,
,
解得:n=90,
∴∠EOP=90°,
由(1)得:當窗戶完全閉合時,∠POC=180°﹣60°=150°,
∴∠COE=150°﹣90°=60°,
∴∠BOC=90°﹣60°=30°,
∴∠ABC=60°,
∴△ABC是等邊三角形,BC=OA=20,
∵BP=AB+OA+OP=45,
![]()
∴CG=BG﹣BC=![]() ,
,
在Rt△PCG中,由勾股定理得: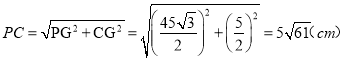 .
.
故答案為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】我們規定:若拋物線的頂點在坐標軸上,則稱該拋物線為“數軸函數”例如拋物線y=x2和y=(x-1)2都是“數軸函數”.
(1)拋物線y=x2-4x+4和拋物線y=x2-6x是“數軸函數“嗎?請說明理由;
(2)若拋物線y=2x2+4mx+m2+16是“數軸函數”,求該拋物線的表達式
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,直線
,直線![]() :
:![]() 交
交![]() 軸于點
軸于點![]() ,交直線
,交直線![]() 點
點![]() .
.
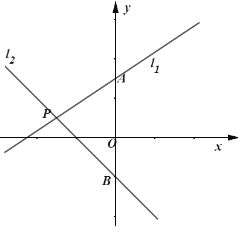
(1)求直線![]() 的函數解析式;
的函數解析式;
(2)過動點![]() 作
作![]() 軸的垂線與直線
軸的垂線與直線![]() 、
、![]() 分別交于
分別交于![]() 、
、![]() 兩點,且
兩點,且![]() .
.
①求![]() 的取值范圍;
的取值范圍;
②若![]() ,直接寫出
,直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
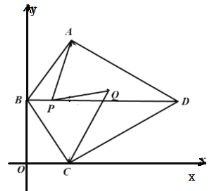
【題目】如圖,在四邊形![]() 中,
中,![]() ,
,![]() ,對角線
,對角線![]() ,點
,點![]() 在
在![]() 軸上,
軸上,![]() 與
與![]() 軸平行,點
軸平行,點![]() 在
在![]() 軸上.
軸上.
(1)求![]() 的度數.
的度數.
(2)點![]() 在對角線
在對角線![]() 上,點
上,點![]() 在四邊形
在四邊形![]() 內且在點
內且在點![]() 的右邊,連接
的右邊,連接![]() ,已知
,已知![]() ,
,![]() ,設
,設![]() .
.
①求![]() 的長(用含
的長(用含![]() 的代數式表示);
的代數式表示);
②若某一反比例函數圖象同時經過點![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解七年級學生體育測試情況,在七年級各班隨機抽取了部分學生的體育測試成績,按![]() 四個等級進行統計(說明:
四個等級進行統計(說明:![]() 級:90分~100分;
級:90分~100分;![]() 級:75分~89分;
級:75分~89分;![]() 級:60分~74分;
級:60分~74分;![]() 級:60分以下),并將統計結果繪制成兩個不完整的統計圖,請你結合統計圖中所給信息解答下列問題:
級:60分以下),并將統計結果繪制成兩個不完整的統計圖,請你結合統計圖中所給信息解答下列問題:
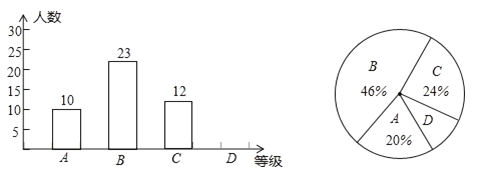
(1)學校在七年級各班共隨機調查了________名學生;
(2)在扇形統計圖中,![]() 級所在的扇形圓心角的度數是_________;
級所在的扇形圓心角的度數是_________;
(3)請把條形統計圖補充完整;
(4)若該校七年級有500名學生,請根據統計結果估計全校七年級體育測試中![]() 級學生約有多少名?
級學生約有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() ,點
,點![]() 是
是![]() 的中點,點
的中點,點![]() 為對角線
為對角線![]() 上的動點,設
上的動點,設![]() ,作
,作![]() 于點
于點![]() ,連結
,連結![]() 并延長至點
并延長至點![]() ,使得
,使得![]() ,作點
,作點![]() 關于
關于![]() 的對稱點
的對稱點![]() ,
,![]() 交
交![]() 于點
于點![]() ,連結
,連結![]() .
.
(1)求證:![]() ;
;
(2)當點![]() 運動到對角線
運動到對角線![]() 的中點時,求
的中點時,求![]() 的周長;
的周長;
(3)在點![]() 的運動的過程中,
的運動的過程中,![]() 是否可以為等腰三角形?若可以,求出
是否可以為等腰三角形?若可以,求出![]() 的值;若不可以,說明理由.
的值;若不可以,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了調查學生對垃圾分類及投放知識的了解情況,從甲、乙兩校各隨機抽取40名學生進行了相關知識測試,獲得了他們的成績(百分制),并對數據(成績)進行了整理、描述和分析.下面給出了部分信息.
a.甲、乙兩校40名學生成績的頻數分布統計表如下:
成績x 學校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(說明:成績80分及以上為優秀,70~79分為良好,60~69分為合格,60分以下為不合格)
b.甲校成績在![]() 這一組的是:
這一組的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙兩校成績的平均分、中位數、眾數如下:
學校 | 平均分 | 中位數 | 眾數 |
甲 | 74.2 | n | 5 |
乙 | 73.5 | 76 | 84 |
根據以上信息,回答下列問題:
(1)寫出表中n的值;
(2)在此次測試中,某學生的成績是74分,在他所屬學校排在前20名,由表中數據可知該學生是_____________校的學生(填“甲”或“乙”),理由是__________;
(3)假設乙校800名學生都參加此次測試,估計成績優秀的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AD是⊙O的直徑,弧BA=弧BC,BD交AC于點E,點F在DB的延長線上,且∠BAF=∠C.
(1)求證:AF是⊙O的切線;
(2)求證:△ABE∽△DBA;
(3)若BD=8,BE=6,求AB的長.
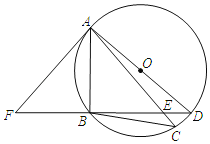
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某數學活動小組在一次活動中,對一個數學問題作如下探究:
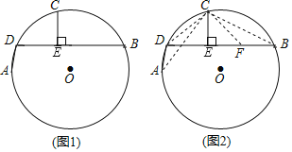
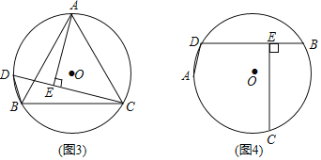
(問題發現)如圖1,AD,BD為⊙O的兩條弦(AD<BD),點C為![]() 的中點,過C作CE⊥BD,垂足為E.求證:BE=DE+AD.
的中點,過C作CE⊥BD,垂足為E.求證:BE=DE+AD.
(問題探究)小明同學的思路是:如圖2,在BE上截取BF=AD,連接CA,CB,CD,CF.……請你按照小明的思路完成上述問題的證明過程.
(結論運用)如圖3,△ABC是⊙O的內接等邊三角形,點D是![]() 上一點,∠ACD=45°,連接BD,CD,過點A作AE⊥CD,垂足為E.若AB=
上一點,∠ACD=45°,連接BD,CD,過點A作AE⊥CD,垂足為E.若AB=![]() ,則△BCD的周長為 .
,則△BCD的周長為 .
(變式探究)如圖4,若將(問題發現)中“點C為![]() 的中點”改為“點C為優弧
的中點”改為“點C為優弧![]() 的中點”,其他條件不變,上述結論“BE=DE+AD”還成立嗎?若成立,請說明理由;若不成立,請寫出BE、AD、DE之間的新等量關系,并加以證明.
的中點”,其他條件不變,上述結論“BE=DE+AD”還成立嗎?若成立,請說明理由;若不成立,請寫出BE、AD、DE之間的新等量關系,并加以證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com