
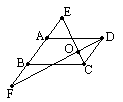
如圖,已知平行四邊形ABCD中,2AB=AD,AB=AE=BF.
求證:EC⊥FD.
|
證明:∵四邊形ABCD是平行四邊形, ∴AB∥DC,AD∥BC,AD=BC. 又∵2AB=AD,AB=AE=BF, ∴BE=BC,AD=AF, ∴∠E=∠BCE,∠F=∠ADF.(等腰三角形中兩個底角相等) ∵AB∥DC, ∴∠E=∠DCE,∠F=∠CDF, ∴∠BCE=∠DCE,∠ADF=∠CDF. 又∵∠ADC+∠BCD= ∴∠CDF+∠DCE= ∴∠DOC= 即EC⊥FD. 思路分析:由題目條件可知本題主要運用平行四邊形的性質(zhì)及等腰三角形的性質(zhì). |


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:初中數(shù)學 來源: 題型:
 CD的邊長a等于點P,Q間的距離.
CD的邊長a等于點P,Q間的距離.| CG | CB |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
 如圖,已知平行四邊形ABCD的對角線AC,BD相交于點O,BD繞點O順時針旋轉交AB,DC于E,F(xiàn).
如圖,已知平行四邊形ABCD的對角線AC,BD相交于點O,BD繞點O順時針旋轉交AB,DC于E,F(xiàn).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
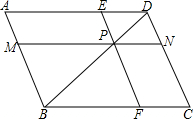 交AB、CD、AD、BC于M、N、E、F,設a=PM•PE,b=PN•PF.
交AB、CD、AD、BC于M、N、E、F,設a=PM•PE,b=PN•PF.| BP |
| PD |
| S平行四邊形PEAM |
| S△ABD |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
 23、如圖,已知平行四邊形ABCD.
23、如圖,已知平行四邊形ABCD.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
 如圖,已知平行四邊形ABCD,作DE⊥AB,垂足為E,把三角形AED沿AB方向平移AB長個單位長度.
如圖,已知平行四邊形ABCD,作DE⊥AB,垂足為E,把三角形AED沿AB方向平移AB長個單位長度.查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com