
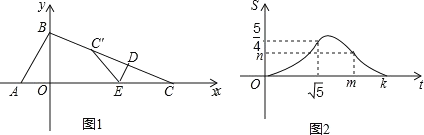
【題目】如圖 1,直線 y=2x+2 分別交 x 軸、y 軸于點A、B,點C為x軸正半軸上的點,點 D從點C處出發,沿線段CB勻速運動至點 B 處停止,過點D作DE⊥BC,交x軸于點E,點 C′是點C關于直線DE的對稱點,連接 EC′,若△ DEC′與△ BOC 的重疊部分面積為S,點D的運動時間為t(秒),S與 t 的函數圖象如圖 2 所示.
(1)VD ,C 坐標為 ;
(2)圖2中,m= ,n= ,k= .
(3)求出S與t 之間的函數關系式(不必寫自變量t的取值范圍).
【答案】(1)點D的運動速度為1單位長度/秒,點C坐標為(4,0).(2)![]() ;
;![]() ;
;![]() .(3)①當點C′在線段BC上時, S=
.(3)①當點C′在線段BC上時, S=![]() t2;②當點C′在CB的延長線上, S=
t2;②當點C′在CB的延長線上, S=![]() t2+
t2+![]() t
t![]() ;③當點E在x軸負半軸, S=t24
;③當點E在x軸負半軸, S=t24![]() t+20.
t+20.
【解析】
(1)根據直線的解析式先找出點B的坐標,結合圖象可知當t=![]() 時,點C′與點B重合,通過三角形的面積公式可求出CE的長度,結合勾股定理可得出OE的長度,由OC=OE+EC可得出OC的長度,即得出C點的坐標,再由勾股定理得出BC的長度,根據CD=
時,點C′與點B重合,通過三角形的面積公式可求出CE的長度,結合勾股定理可得出OE的長度,由OC=OE+EC可得出OC的長度,即得出C點的坐標,再由勾股定理得出BC的長度,根據CD=![]() BC,結合速度=路程÷時間即可得出結論;
BC,結合速度=路程÷時間即可得出結論;
(2)結合D點的運動以及面積S關于時間t的函數圖象的拐點,即可得知當“當t=k時,點D與點B重合,當t=m時,點E和點O重合”,結合∠C的正余弦值通過解直角三角形即可得出m、k的值,再由三角形的面積公式即可得出n的值;
(3)隨著D點的運動,按△DEC′與△BOC的重疊部分形狀分三種情況考慮:①通過解直角三角形以及三角形的面積公式即可得出此種情況下S關于t的函數關系式;②由重合部分的面積=S△CDES△BC′F,通過解直角三角形得出兩個三角形的各邊長,結合三角形的面積公式即可得出結論;③通過邊與邊的關系以及解直角三角形找出BD和DF的值,結合三角形的面積公式即可得出結論.
(1)令x=0,則y=2,即點B坐標為(0,2),
∴OB=2.
當t=![]() 時,B和C′點重合,如圖1所示,
時,B和C′點重合,如圖1所示,
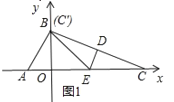
此時S=![]() ×
×![]() CEOB=
CEOB=![]() ,
,
∴CE=![]() ,
,
∴BE=![]() .
.
∵OB=2,
OE=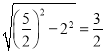 ,
,
∴OC=OE+EC=![]() +
+![]() =4,BC=
=4,BC=![]() ,CD=
,CD=![]() ,
,
![]() ÷
÷![]() =1(單位長度/秒),
=1(單位長度/秒),
∴點D的運動速度為1單位長度/秒,點C坐標為(4,0).
故答案為:1單位長度/秒;(4,0);
(2)根據圖象可知:
當t=k時,點D與點B重合,
此時k=![]() =2
=2![]() ;
;
當t=m時,點E和點O重合,如圖2所示.
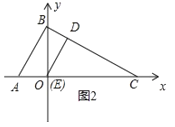
sin∠C=![]() =
=![]() =
=![]() ,cos∠C=
,cos∠C=![]() ,
,
OD=OCsin∠C=4×![]() =
=![]() ,CD=OCcos∠C=4×
,CD=OCcos∠C=4×![]() =
=![]() .
.
∴m=![]() =
=![]() ,n=
,n=![]() BDOD=
BDOD=![]() ×(2
×(2![]()
![]() )×
)×![]() =
=![]() .
.
故答案為:![]() ;
;![]() ;2
;2![]() .
.
(3)隨著D點的運動,按△DEC′與△BOC的重疊部分形狀分三種情況考慮:
①當點C′在線段BC上時,如圖3所示.
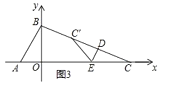
此時CD=t,CC′=2t,0<CC′≤BC,
∴0<t≤![]() .
.
∵tan∠C=![]() ,
,
∴DE=CDtan∠C=![]() t,
t,
此時S=![]() CDDE=
CDDE=![]() t2;
t2;
②當點C′在CB的延長線上,點E在線段OC上時,如圖4所示.

此時CD=t,BC′=2t2![]() ,DE=CDtan∠C=
,DE=CDtan∠C=![]() t,CE=
t,CE=![]() =
=![]() t,OE=OCCE=4
t,OE=OCCE=4![]() t,
t,
∵![]() ,即
,即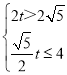 ,
,
解得:![]() <t≤
<t≤![]() .
.
由(1)可知tan∠OEF=![]() =
=![]() ,
,
∴OF=OEtan∠OEF=![]() t,BF=OBOF=
t,BF=OBOF=![]() ,
,
∴FM=BFcos∠C=![]() .
.
此時S=![]() CDDE
CDDE![]() BC′FM=
BC′FM=![]() ;
;
③當點E在x軸負半軸,點D在線段BC上時,如圖5所示.
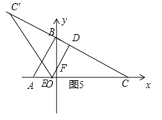
此時CD=t,BD=BCCD=2![]() t,CE=
t,CE=![]() t,DF=
t,DF=![]() ,
,
∵![]() ,即
,即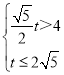 ,
,
∴![]() <t≤2
<t≤2![]() .
.
此時S=![]() BDDF=
BDDF=![]() ×2×(2
×2×(2![]() t)2=t24
t)2=t24![]() t+20.
t+20.
綜上,當點C′在線段BC上時, S=![]() t2;當點C′在CB的延長線上, S=
t2;當點C′在CB的延長線上, S=![]() t2+
t2+![]() t
t![]() ;當點E在x軸負半軸, S=t24
;當點E在x軸負半軸, S=t24![]() t+20.
t+20.


科目:初中數學 來源: 題型:
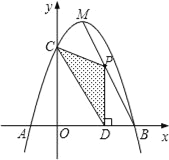
【題目】如圖,拋物線y=﹣x2+bx+c與x軸相交于A、B兩點,與y軸相交于點C,且點B與點C的坐標分別為B(3,0).C(0,3),點M是拋物線的頂點.
(1)求二次函數的關系式;
(2)點P為線段MB上一個動點,過點P作PD⊥x軸于點D.若OD=m,△PCD的面積為S,試判斷S有最大值或最小值?并說明理由;
(3)在MB上是否存在點P,使△PCD為直角三角形?如果存在,請求出點P的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將函數![]() 的圖象位于
的圖象位于![]() 軸下方的部分沿
軸下方的部分沿![]() 軸翻折至其上方后,所得的是新函數
軸翻折至其上方后,所得的是新函數![]() 的圖象.若該新函數圖象與直線
的圖象.若該新函數圖象與直線![]() 有兩個交點,則
有兩個交點,則![]() 的取值范圍為___________.
的取值范圍為___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
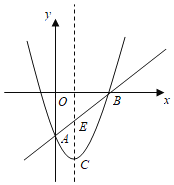
【題目】如圖,在平面直角坐標系![]() 中,已知拋物線
中,已知拋物線![]() 與直線
與直線![]() 都經過
都經過![]() 、
、![]() 兩點,該拋物線的頂點為C.
兩點,該拋物線的頂點為C.
(1)求此拋物線和直線![]() 的解析式;
的解析式;
(2)設直線![]() 與該拋物線的對稱軸交于點E,在射線
與該拋物線的對稱軸交于點E,在射線![]() 上是否存在一點M,過M作x軸的垂線交拋物線于點N,使點M、N、C、E是平行四邊形的四個頂點?若存在,求點M的坐標;若不存在,請說明理由;
上是否存在一點M,過M作x軸的垂線交拋物線于點N,使點M、N、C、E是平行四邊形的四個頂點?若存在,求點M的坐標;若不存在,請說明理由;
(3)設點P是直線![]() 下方拋物線上的一動點,當
下方拋物線上的一動點,當![]() 面積最大時,求點P的坐標,并求
面積最大時,求點P的坐標,并求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
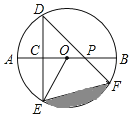
【題目】如圖,AB是⊙O的直徑,弦DE垂直平分半徑OA,C為垂足,弦DF與半徑OB相交于點P,連接EF、EO,若DE=2,∠DPA=45°.
(1)求⊙O的半徑;
(2)求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
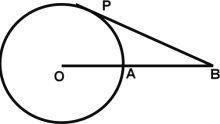
【題目】如圖,圓O的半徑為3cm,B為圓O外一點,OB交圓O于A,AB=OA,動點P從點A出發,以πcm/s的速度在圓O上按逆時針方向運動一周回到點A立即停止.當點P運動的時間為( )秒時,BP與圓O相切.
A.1sB.5sC.1s或 5sD.2s或 4s
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠MAN=60°,點B在射線AM上,AB=4,點P為直線AN上一動點,以BP為邊作等邊三角形BPQ(點B,P,Q按順時針排列),點O是△BPQ的外心.
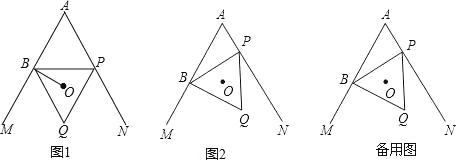
(1)如圖1,當OB⊥AM時,點O________∠MAN的平分線上(填“在”或“不在”);
(2)求證:當點P在射線AN上運動時,總有點O在∠MAN的平分線;
(3)當點P在射線AN上運動(點P與點A不重合)時,AO與BP交于點C,設AP=m,用m表示AC·AO;
(4)若點D在射線AN上,AD=2,圓I為△ABD的內切圓.當△BPQ的邊BP或BQ與圓I相切時,請直接寫出點A與點O的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
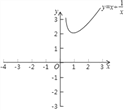
【題目】某數學興趣小組對函數y=x+![]() 的圖象和性質進行了探究,探究過程如下,請補充完整.
的圖象和性質進行了探究,探究過程如下,請補充完整.
x | … | ﹣3 | ﹣2 | ﹣1 | - | - |
|
| 1 | 2 | 3 | … |
y | … | - | m | ﹣2 | - | - |
|
| 2 |
|
| … |
(1)自變量x的取值范圍是 ,m= .
(2)根據(1)中表內的數據,在如圖所示的平面直角坐標系中描點,畫出函數圖象的一部分,請你畫出該函數圖象的另一部分.
(3)請你根據函數圖象,寫出兩條該函數的性質;
(4)進一步探究該函數的圖象發現:
①方程x+![]() =3有 個實數根;
=3有 個實數根;
②若關于x的方程x+![]() =t有2個實數根,則t的取值范圍是 .
=t有2個實數根,則t的取值范圍是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
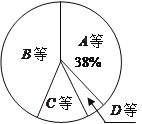
【題目】某校為了解九年級男生1000米長跑的成績,從中隨機抽取了50名男生進行測試,根據測試評分標準,將他們的得分進行統計后分為A、B、C、D四等,并繪制成下面的頻數分布表和扇形統計圖.
等第 | 成績(得分) | 頻數(人數) | 頻率 |
A | 10分 | 7 | 0.14 |
9分 | x | m | |
B | 8分 | 15 | 0.30 |
7分 | 8 | 0.16 | |
C | 6分 | 4 | 0.08 |
5分 | y | n | |
D | 5分以下 | 3 | 0.06 |
合計 | 50 | 1.00 |
(1)試直接寫出
(2)求表示得分為C等的扇形的圓心角的度數;
(3)如果該校九年級共有男生200名,試估計這200名男生中成績達到A等和B等的人數共有多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com