
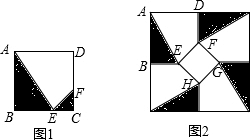
 BC和CD上,若將此種地磚按圖2所示的形式鋪設,能使中間的深色陰影部分成四邊形EFGH.
BC和CD上,若將此種地磚按圖2所示的形式鋪設,能使中間的深色陰影部分成四邊形EFGH. CE×CF=0.5x2
CE×CF=0.5x2 AB×BE=
AB×BE= ×0.4×(0.4-x)=0.08-0.2x
×0.4×(0.4-x)=0.08-0.2x

 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
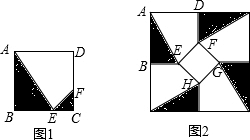 BC和CD上,若將此種地磚按圖2所示的形式鋪設,能使中間的深色陰影部分成四邊形EFGH.
BC和CD上,若將此種地磚按圖2所示的形式鋪設,能使中間的深色陰影部分成四邊形EFGH.查看答案和解析>>
科目:初中數學 來源:2009年福建省泉州市安溪縣初中學業質量檢查數學試卷(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com