Question

【題目】如圖1，已知，點、在直線上，點、在直線上，且于.

（1）求證：；

（2）如圖2，平分交于點，平分交于點，求的度數；

（3）如圖3，為線段上一點，為線段上一點，連接，為的角平分線上一點，且，則、、之間的數量關系是__________.

Answer 1

【答案】（1）見解析；（2）225°；（3）或

【解析】

(1) 過作EF∥a,由BC⊥AD可知，由平行可知，，從而可得=+=

(2)作，，設，，由平行線性質和鄰補角定義可得，，進而計算出即可解答，

（3）分兩種情況解答：I.∠NCD在∠BCD內部，II外部，仿照（2）解答即可.

（1）證明：過作,

　

∴

　

∴

　

∴

　

∴

∴

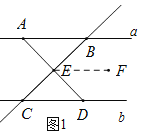
（2）解：作，，

設，，

由（1）知：，，

，

∴，

∴，

同理：，

∴

（3）結論：或，

I.∠NCD在∠BCD內部時，

過I點作，過N點作，設∠IPN=∠BPN=x，=y，

∴∠BCD=3y.

∵a∥b，

∴

∴，，，

∴，，

∴，

∴

∴

II.在外部時,如圖3（2）：

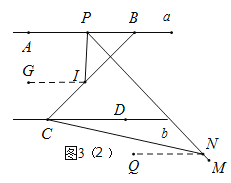
過I點作，過N點作，設∠IPN=∠BPN=x，=y，

∴∠BCD=y.

∵a∥b，

∴IG∥a∥

∴，，，

∴，，

∴，

∴

∴