
【題目】如圖1,O為線段AB上一點,AB=6,OC為射線,且∠BOC=60°,動點P以每秒2個單位長度的速度從點O出發,沿射線OC做勻速運動,設運動時間為t秒.
(1)若AO=4,
①當t=1秒時,OP= , S△ABP=;
②當△ABP是直角三角形時,求t的值;
(2)如圖2,若點O為AB中點,當AP=AB時,過點A作AQ∥BP,并使得∠QOP=∠B,求AQBP的值.
【答案】
(1)2,3 ![]() ,解:②當△ABP是直角三角形時,a、若∠A=90°.∵∠BOC=60°且∠BOC>∠A,∴∠A≠90°,故此種情形不存在;b、若∠B=90°,如答圖2所示:
,解:②當△ABP是直角三角形時,a、若∠A=90°.∵∠BOC=60°且∠BOC>∠A,∴∠A≠90°,故此種情形不存在;b、若∠B=90°,如答圖2所示: ∵∠BOC=60°,∴∠BPO=30°,∴OP=2OB=4,又OP=2t,∴t=2;c、若∠APB=90°,如答圖3所示:
∵∠BOC=60°,∴∠BPO=30°,∴OP=2OB=4,又OP=2t,∴t=2;c、若∠APB=90°,如答圖3所示: 過點P作PD⊥AB于點D,則OD=OP?sin30°=t,PD=OP?sin60°=
過點P作PD⊥AB于點D,則OD=OP?sin30°=t,PD=OP?sin60°= ![]() t,∴AD=OA+OD=4+t,BD=OB﹣OD=2﹣t.在Rt△ABP中,由勾股定理得:PA2+PB2=AB2∴(AD2+PD2)+(BD2+PD2)=AB2,即[(4+t)2+(
t,∴AD=OA+OD=4+t,BD=OB﹣OD=2﹣t.在Rt△ABP中,由勾股定理得:PA2+PB2=AB2∴(AD2+PD2)+(BD2+PD2)=AB2,即[(4+t)2+( ![]() t)2]+[(2﹣t)2+(
t)2]+[(2﹣t)2+( ![]() t)2]=62,解方程得:t=
t)2]=62,解方程得:t= ![]() 或t=
或t= ![]() (負值舍去),∴t=
(負值舍去),∴t= ![]() .綜上所述,當△ABP是直角三角形時,t=2或t=
.綜上所述,當△ABP是直角三角形時,t=2或t= ![]() .
.
(2)解:如圖中,作OE∥AP,交BP于點E.

∵AP=AB,
∴∠APB=∠B,
∴∠OEB=∠APB=∠B,
∵AQ∥BP,
∴∠QAB+∠B=180°.
又∵∠OEP+∠OEB=180°,
∴∠OEP=∠QAB,
又∵∠AOC=∠2+∠B=∠1+∠QOP,
∵∠B=∠QOP,
∴∠AOQ=∠OPE,
∴△QAO∽△OEP,
∴ ![]() =
= ![]() ,即AQEP=EOAO,
,即AQEP=EOAO,
由三角形中位線定理得OE=3,
∴AQEP=9,
∴AQBP=AQ2EP=2AQEP=18.
【解析】解:(1)①當t=1秒時,OP=2t=2×1=2.
如答圖1,過點P作PD⊥AB于點D.

在Rt△POD中,PD=OPsin60°=2× ![]() =
= ![]() ,
,
∴S△ABP= ![]() ABPD=
ABPD= ![]() ×(4+2)×
×(4+2)× ![]() =3
=3 ![]() .
.
所以答案是2,3 ![]() .
.
【考點精析】關于本題考查的等腰三角形的性質和勾股定理的概念,需要了解等腰三角形的兩個底角相等(簡稱:等邊對等角);直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2才能得出正確答案.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某車間為了改變管理松懈的狀況,準備采取每天任務定額和超產有獎的措施,從而提高工作效率.下面是該車間15名工人過去一天中各自裝配機器的數量(單位:臺):
15,6,16,7,15,8,7,13,8,11,8,10,9,10,9.
請回答下列問題:
(1)這組數據的平均數、眾數和中位數各是多少(結果精確到0.01臺)?
(2)管理者應確定每人標準日產量為多少臺比較合適?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果把一個奇數位的自然數各數為上的數字從最高位到個位依次排列,與從個位到最高位依次排列出的一串數字完全相同,相鄰兩個數位上的數字之差的絕對值相等(不等于0),且該數正中間的數字與其余數字均不同,我們把這樣的自然數稱為“階梯數”,例如自然數12321,從最高位到個位依次排出的一串數字是:1,2,3,2,1,從個位到最高位依次排出的一串數字仍是:1,2,3,2,1,且|1﹣2|=|2﹣3|=|3﹣2|=|2﹣1|=1,因此12321是一個“階梯數”,又如262,85258,…,都是“階梯數”,若一個“階梯數”t從左數到右,奇數位上的數字之和為M,偶數位上的數字之和為N,記P(t)=2N﹣M,Q(t)=M+N.
(1)已知一個三位“階梯數”t,其中P(t)=12,且Q(t)為一個完全平方數,求這個三位數;
(2)已知一個五位“階梯數”t能被4整除,且Q(t)除以4余2,求該五位“階梯數”t的最大值與最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
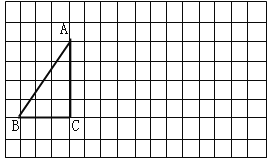
【題目】將下列方格紙中的△ABC向右平移7格,再向下平移2格,得到△![]() .(1)畫出平移后的三角形;
.(1)畫出平移后的三角形;
(2)若AB=5,則![]() = .
= .
(3)連接AA1,BB1, 根據“圖形平移”的性質,得:線段AA1與線段BB1的數量關系和位置關系是: .
(4)求圖中∠![]() AC+∠
AC+∠![]() BC的度數.
BC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了了解初中各年級學生每天的平均睡眠時間(單位:h,精確到1 h),抽樣調查了部分學生,并用得到的數據繪制了下面兩幅不完整的統計圖.
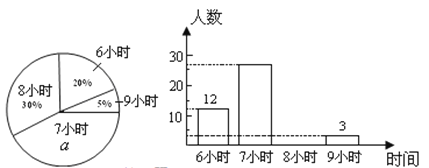
請你根據圖中提供的信息,回答下列問題:
(1)求出扇形統計圖中百分數![]() 的值為_______,所抽查的學生人數為______;
的值為_______,所抽查的學生人數為______;
(2)求出平均睡眠時間為8小時的人數,并補全條形圖;
(3)求出這部分學生的平均睡眠時間的平均數;
(4)如果該校共有學生1200名,請你估計睡眠不足(少于8小時)的學生數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于![]() 的方程組
的方程組![]() ,以下結論:
,以下結論:
①![]() 時,方程組的解也是方程
時,方程組的解也是方程![]() 的解;
的解;
②論![]() 取什么實數,
取什么實數,![]() 的值始終不變;
的值始終不變;
③若![]() ,則
,則![]() 的最小值為
的最小值為![]() ;
;
請判斷以上結論是否正確,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com