
【題目】已知拋物線![]() (
(![]() 是常數)與
是常數)與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() .
.
(Ⅰ)當![]() 時,求拋物線的解析式及頂點坐標;
時,求拋物線的解析式及頂點坐標;
(Ⅱ)在(Ⅰ)的條件下,![]() 為拋物線上的一個動點.
為拋物線上的一個動點.
①求當![]() 關于原點的對稱點
關于原點的對稱點![]() 落在直線
落在直線![]() 上時,求
上時,求![]() 的值;
的值;
②當![]() 關于原點的對稱點
關于原點的對稱點![]() 落在第一象限內,
落在第一象限內,![]() 取得最小值時,求
取得最小值時,求![]() 的值及這個最小值.
的值及這個最小值.
【答案】(Ⅰ)![]() ,拋物線的頂點坐標為
,拋物線的頂點坐標為![]() ; (Ⅱ)①
; (Ⅱ)①![]() 的值為
的值為![]() 或
或![]() ;②
;②![]() 的值為
的值為![]() ,
,![]() 的最小值為
的最小值為![]()
【解析】
(Ⅰ)用待定系數法求出b、c即可得出解析式和頂點坐標;
(Ⅱ)①先用待定系數法求出直線BC的解析式,由于點P’與點P(m,t)關于原點對稱,故點P’的坐標為(-m,-t),將其代入直線BC解析式,即可求解;
②點P’落在第一象限可得m<0,t<0,連接AP’,過點P’作P’H⊥x軸于點H,則H(-m,0),可得在Rt△P’AH中,![]() ,可以得到
,可以得到![]() 的長度關于m的函數關系式,通過配方法可以求出
的長度關于m的函數關系式,通過配方法可以求出![]() 的最小值.
的最小值.
(Ⅰ)∵拋物線![]() 經過點A(-1,0)C(0,-3),
經過點A(-1,0)C(0,-3),
∴![]() ,解得
,解得![]() .
.
∴拋物線的解析式為![]()
∵![]() ,
,
∴拋物線的頂點坐標為(1,-4).
(Ⅱ)①由(Ⅰ)可知![]() 與x軸交點B的坐標為(3,0),與y軸交點C的坐標為(0,-3).
與x軸交點B的坐標為(3,0),與y軸交點C的坐標為(0,-3).
設直線BC的解析式為y=kx+b(k![]() 0),
0),
∴![]() .解得
.解得![]() .
.
∴直線BC的解析式為y=x-3.
∵點P’與點P(m,t)關于原點對稱,∴點P’的坐標為(-m,-t).
∵點P關于原點的對稱點P’ (-m,-t)落在直線BC上,
∴-t=-m-3,即t=m+3.
∵點P(m,t)在拋物線![]() 上,∴
上,∴![]() .
.
∴![]() .解得
.解得![]() 或
或![]() .
.
∴![]() 的值為
的值為![]() 或
或![]() .
.
②∵點P(m,t)關于原點的對稱點P’ (-m,-t)落在第一象限內,
∴-m>0,-t>0,即m<0,t<0.
∵點P(m,t)在拋物線![]() 上,∴
上,∴![]() ..
..
∴![]()
連接AP’,過點P’作P’H⊥x軸于點H,則H(-m,0).
∵A(-1,0),∴![]() .
.
∵在Rt△P’AH中,![]() ,
,
∴![]() ,
,
∵1>0,∴當![]() 時,
時,![]() 有最小值
有最小值![]() .
.
∴![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
∴![]() 的值為
的值為![]() ,
,![]() 的最小值為
的最小值為![]() .
.


科目:初中數學 來源: 題型:
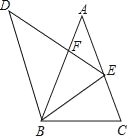
【題目】如圖,在△ABC中,∠A=36°,AC=AB=2,將△ABC繞點B逆時針方向旋轉得到△DBE,使點E在邊AC上,DE交AB于點F,則△AFE與△DBF的面積之比等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
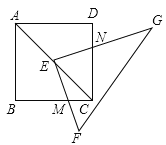
【題目】如圖,點E在正方形ABCD的對角線AC上,且EC=2AE,Rt△FEG的兩直角邊EF、EG分別交BC、DC于點M、N.若正方形ABCD的邊長為6,則重疊部分四邊形EMCN的面積為( )
A.24B.9C.20D.16
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線![]() 的頂點為
的頂點為![]() ,與直線
,與直線![]() 相交于點
相交于點![]() ,點
,點![]() 關于直線
關于直線![]() 的對稱點為
的對稱點為![]() .
.
(Ⅰ)若拋物線![]() 經過原點,求
經過原點,求![]() 的值;
的值;
(Ⅱ)是否存在![]() 的值,使得點
的值,使得點![]() 到
到![]() 軸距離等于點
軸距離等于點![]() 到直線
到直線![]() 距離的一半,若存在,請直接寫出
距離的一半,若存在,請直接寫出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(Ⅲ)將![]() 的函數圖象記為圖象
的函數圖象記為圖象![]() ,圖象
,圖象![]() 關于直線
關于直線![]() 的對稱圖象記為圖象
的對稱圖象記為圖象![]() ,圖象
,圖象![]() 與圖象
與圖象![]() 組合成的圖象記為
組合成的圖象記為![]() .
.
①當![]() 與
與![]() 軸恰好有三個交點時,求
軸恰好有三個交點時,求![]() 的值:
的值:
②當![]() 為等邊三角形時,直接寫出
為等邊三角形時,直接寫出![]() 所對應的函數值小于0時,自變量
所對應的函數值小于0時,自變量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市開展“美麗家鄉,創衛同行”活動,某校倡議學生利用雙休日參加義務勞動,為了解同學們勞動情況,學校隨機調查了部分同學的勞動時間,并用得到的數據繪制了不完整的統計圖①和圖②,請根據相關信息,解答下列問題:
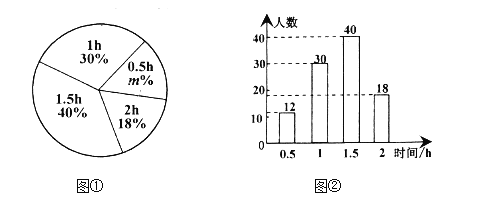
(Ⅰ)本次接受隨機抽樣調查的學生人數為 ,圖①中![]() 的值是 ;
的值是 ;
(Ⅱ)求本次調查獲取的樣本數據的平均數、眾數和中位數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據《居民家庭親子閱讀消費調查報告》中的相關數據制成扇形統計圖,由圖可知,下列說法錯誤的是( )

A.扇形統計圖能反映各部分在總體中所占的百分比
B.每天閱讀30分鐘以上的居民家庭孩子超過50%
C.每天閱讀1小時以上的居民家庭孩子占20%
D.每天閱讀30分鐘至1小時的居民家庭孩子對應扇形的圓心角是108°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在圖1,2,3中,已知![]() ,
,![]() ,點
,點![]() 為線段
為線段![]() 上的動點,連接
上的動點,連接![]() ,以
,以![]() 為邊向上作菱形
為邊向上作菱形![]() ,且
,且![]() .
.
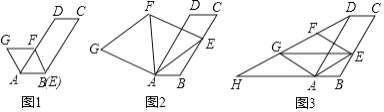
(1)如圖1,當點![]() 與點
與點![]() 重合時,
重合時,![]() ________°;
________°;
(2)如圖2,連接![]() .
.
①填空:![]() _________
_________![]() (填“>”,“<”,“=”);
(填“>”,“<”,“=”);
②求證:點![]() 在
在![]() 的平分線上;
的平分線上;
(3)如圖3,連接![]() ,
,![]() ,并延長
,并延長![]() 交
交![]() 的延長線于點
的延長線于點![]() ,當四邊形
,當四邊形![]() 是平行四邊形時,求
是平行四邊形時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線![]() (b,c為常數)與x軸交于點
(b,c為常數)與x軸交于點![]() 和
和![]() ,與y軸交于點A,點E為拋物線頂點。
,與y軸交于點A,點E為拋物線頂點。
(Ⅰ)當![]() 時,求點A,點E的坐標;
時,求點A,點E的坐標;
(Ⅱ)若頂點E在直線![]() 上,當點A位置最高時,求拋物線的解析式;
上,當點A位置最高時,求拋物線的解析式;
(Ⅲ)若![]() ,當
,當![]() 滿足
滿足![]() 值最小時,求b的值。
值最小時,求b的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com