【題目】某學校是乒乓球體育傳統項目學校，為進一步推動該項目的開展，學校準備到體育用品店購買直拍球拍和橫拍球拍若干副，并且每買一副球拍必須要買10個乒乓球，乒乓球的單價為2元/個，若購買20副直拍球拍和15副橫拍球拍花費9000元；購買10副橫拍球拍比購買5副直拍球拍多花費1600元．
（1）求兩種球拍每副各多少元？
（2）若學校購買兩種球拍共40副，且直拍球拍的數量不多于橫拍球拍數量的3倍，請你給出一種費用最少的方案，并求出該方案所需費用．
【答案】（1）直拍球拍每副220元，橫拍球每副260元；（2）購買直拍球拍30副，則購買橫拍球10副時，費用最少．
【解析】（1）設直拍球拍每副x元，根據題中的相等關系：20副直拍球拍的價錢+15副橫拍球拍的價錢＝9000元；10副橫拍球拍價錢－5副直拍球拍價錢＝1600元，建立方程組即可求解；
（2）設購買直拍球拍m副，根據題意列出不等式可得出m的取值范圍，再根據題意列出費用關于m的一次函數，并根據一次函數的性質解答即可.
解：（1）設直拍球拍每副x元，橫拍球每副y元，由題意得，
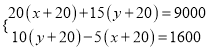
解得， 
，
答：直拍球拍每副220元，橫拍球每副260元；
（2）設購買直拍球拍m副，則購買橫拍球（40-m）副，
由題意得，m≤3（40-m），
解得，m≤30，
設買40副球拍所需的費用為w，
則w=（220+20）m+（260+20）（40-m）
=-40m+11200，
∵-40＜0，
∴w隨m的增大而減小，
∴當m=30時，w取最小值，最小值為-40×30+11200=10000（元）．
答：購買直拍球拍30副，則購買橫拍球10副時，費用最少．
科目：初中數學 來源： 題型：
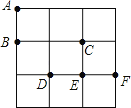
【題目】在3×3的方格紙中，點A、B、C、D、E、F分別位于如圖所示的小正方形的頂點上．
（1）從A、D、E、F四個點中任意取一點，以所取的這一點及點B、C為頂點畫三角形，則所畫三角形是等腰三角形的概率是 ；
（2）從A、D、E、F四個點中先后任意取兩個不同的點，以所取的這兩點及點B、C為頂點畫四邊形，求所畫四邊形是平行四邊形的概率是 （用樹狀圖或列表法求解）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有一個數值轉換器．原理如圖．
⑴當輸入的x為16時．輸出的y是多少？
⑵是否存在輸入有效的x值后，始終輸不出y值？如果存在．請寫出所有滿足要求的x的值；如果不存在，請說明理由；
⑶小明輸入數據，在轉換器運行程序時，屏幕顯示“該操作無法運行”，請你推算輸入的數據可能是什么情況？
⑷若輸出的y是
，試判斷輸入的x值是否唯一？若不唯一，請寫出其中的兩個．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①，在平面直角坐標系中，A（a，0），C（b，4），且滿足（a+4）2+
=0，過C作CB⊥x軸于B．
（1）求三角形ABC的面積．
（2）若線段AC與y軸交于點Q（0，2），在y軸上是否存在點P，使得三角形ABC和三角形QCP的面積相等，若存在，求出P點坐標；若不存在，請說明理由．
（3）若過B作BD∥AC交y軸于D，且AE，DE分別平分∠CAB，∠ODB，如圖②，求∠AED的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法：
①放大（縮小）的圖片與原圖片是相似形；
②比例尺不同的中國地圖是相似形；
③放大鏡下的五角星與原來的五角星是相似形；
④放電影時膠片上的圖像和它映射到屏幕上的圖像是相似形；
⑤平面鏡中，你的像與你本人是相似形．
其中正確的說法有（ ）
A．2個
B．3個
C．4個
D．5個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
