
探究與發現:
(1)探究一:三角形的一個內角與另兩個內角的平分線所夾的角之間的關系
已知:如圖1,在△ADC中,DP、CP分別平分∠ADC和∠ACD,
試探究∠P與∠A的數量關系,并說明理由.
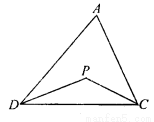
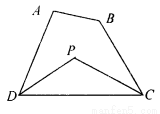
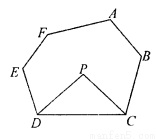
圖1 圖2 圖3
(2)探究二:四邊形的兩個個內角與另兩個內角的平分線所夾的角之間的關系
已知:如圖2,在四邊形ABCD中,DP、CP分別平分∠ADC和∠BCD,試探究∠P與∠A+∠B的數量關系,并說明理由.
(3)探究三:六邊形的四個內角與另兩個內角的平分線所夾的角之間的關系
已知:如圖3,在六邊形ABCDEF中,DP、CP分別平分∠EDC和∠BCD,請直接寫出∠P與∠A+∠B+∠E+∠F的數量關系:__ __ __.
【解析】
試題分析:探究一:根據角平分線的定義可得∠PDC= ∠ADC,∠PCD=
∠ADC,∠PCD= ∠ACD,然后根據三角形內角和定理列式整理即可得解;
∠ACD,然后根據三角形內角和定理列式整理即可得解;
探究二:根據四邊形的內角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可;
探究三:根據六邊形的內角和公式表示出∠ADC+∠BCD,然后同理探究二解答即可.
試題解析:探究一:∵DP、CP分別平分∠ADC和∠ACD,
∴∠PDC= ∠ADC,∠PCD=
∠ADC,∠PCD= ∠ACD,
∠ACD,
∴∠DPC=180°-∠PDC-∠PCD,
=180°- ∠ADC-
∠ADC- ∠ACD,
∠ACD,
=180°- (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°- (180°-∠A),
(180°-∠A),
=90°+ ∠A;
∠A;
探究二:∵DP、CP分別平分∠ADC和∠BCD,
∴∠PDC= ∠ADC,∠PCD=
∠ADC,∠PCD= ∠BCD,
∠BCD,
∴∠DPC=180°-∠PDC-∠PCD,
=180°- ∠ADC-
∠ADC- ∠BCD,
∠BCD,
=180°- (∠ADC+∠BCD),
(∠ADC+∠BCD),
=180°- (360°-∠A-∠B),
(360°-∠A-∠B),
= (∠A+∠B);
(∠A+∠B);
探究三:六邊形ABCDEF的內角和為:(6-2)•180°=720°,
∵DP、CP分別平分∠ADC和∠ACD,
∴∠P= ∠ADC,∠PCD=
∠ADC,∠PCD= ∠ACD,
∠ACD,
∴∠P=180°-∠PDC-∠PCD,
=180°- ∠ADC-
∠ADC- ∠ACD,
∠ACD,
=180°- (∠ADC+∠ACD),
(∠ADC+∠ACD),
=180°- (720°-∠A-∠B-∠E-∠F),
(720°-∠A-∠B-∠E-∠F),
= (∠A+∠B+∠E+∠F)-180°,
(∠A+∠B+∠E+∠F)-180°,
即∠P= (∠A+∠B+∠E+∠F)-180°.
(∠A+∠B+∠E+∠F)-180°.
考點: 1.多邊形內角與外角;2.三角形內角和定理.


 學而優銜接教材南京大學出版社系列答案
學而優銜接教材南京大學出版社系列答案科目:初中數學 來源:2016屆江蘇省興化市七年級下學期期中考試數學試卷(解析版) 題型:選擇題
下列從左到右的變形屬于因式分解的是()
A.x2–2xy+y2=x(x-2y)+y2 B.x2-16y2=(x+8y)(x-8y)
C.x2+xy+y2=(x+y)2 D.x4y4-1=(x2y2+1)(xy+1)(xy-1)
查看答案和解析>>
科目:初中數學 來源:2016屆江蘇泰興楚水實驗中學七年級下學期第一次調研數學卷(解析版) 題型:填空題
在△ABC中,∠C=50°,按圖中虛線將∠C剪去后,∠1+∠2等于______度.

查看答案和解析>>
科目:初中數學 來源:2016屆江蘇無錫市七年級下學期期中考試數學卷(解析版) 題型:解答題
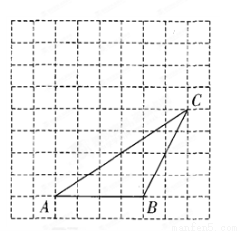
如圖,在每個小正方形邊長為1的方格紙中,△ABC的頂點都在方格紙格點上.將△ABC向左平移2格,再向上平移4格.
(1)請在圖中畫出平移后的△A′B′C′,
(2)再在圖中畫出△A′B′C′的高C′D′,并求出△ABC的面積.
查看答案和解析>>
科目:初中數學 來源:2016屆江蘇揚州中學樹人學校七年級上學期期末考試數學試卷(解析版) 題型:選擇題
如下數表是由從1開始的連續自然數組成,則自然數2014所在的行數是

A.第45行 B.第46行 C.第47行 D.第48行
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com