
【題目】如圖,在平面直角坐標系中,將四邊形ABCD稱為“基本圖形”,且各點的坐標分別為A(4,4),B(1,3),C(3,3),D(3,1).
①畫出“基本圖形”關于原點O對稱的四邊形A1B1C1D1 , 并填出A1 , B1 , C1 , D1的坐標;
②畫出“基本圖形”繞B點順時針旋轉90°所成的四邊形A2B2C2D2
A1( , )B1( , )
C1( , )D1( , )
科目:初中數學 來源: 題型:
【題目】某種水彩筆,在購買時,若同時額外購買筆芯,每個優惠價為3元,使用期間,若備用筆芯不足時需另外購買,每個5元.現要對在購買水彩筆時應同時購買幾個筆芯作出選擇,為此收集了這種水彩筆在使用期內需要更換筆芯個數的30組數據,整理繪制出下面的條形統計圖: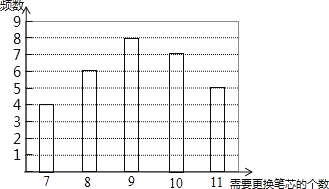
設x表示水彩筆在使用期內需要更換的筆芯個數,y表示每支水彩筆在購買筆芯上所需要的費用(單位:元),n表示購買水彩筆的同時購買的筆芯個數.
(1)若n=9,求y與x的函數關系式;
(2)若要使這30支水彩筆“更換筆芯的個數不大于同時購買筆芯的個數”的頻率不小于0.5,確定n的最小值;
(3)假設這30支筆在購買時,每支筆同時購買9個筆芯,或每支筆同時購買10個筆芯,分別計算這30支筆在購買筆芯所需費用的平均數,以費用最省作為選擇依據,判斷購買一支水彩筆的同時應購買9個還是10個筆芯.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知原點O,A(0,4),B(2,0),將△OAB繞平面內一點P逆時針旋轉90°,使得旋轉后的三角形的兩個頂點恰好落在雙曲線 ![]() 上,則旋轉中心P的坐標為。
上,則旋轉中心P的坐標為。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,∠BCD=45°,將腰CD以點D為中心逆時針旋轉90°至ED,連結AE,CE,則△ADE的面積是( ) 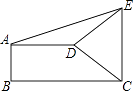
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行于x軸的直線AC分別交拋物線y1=x2(x≥0)與y2= ![]() (x≥0)于B、C兩點,過點C作y軸的平行線交y1于點D,直線DE∥AC,交y2于點E,則
(x≥0)于B、C兩點,過點C作y軸的平行線交y1于點D,直線DE∥AC,交y2于點E,則 ![]() = .
= . 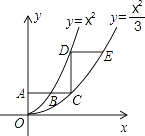
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在△ABC外作△ABD和△ACE,使AD=AB,AE=AC,且∠DAB=∠EAC,連接BE,CD相交于P點,求證:點A在∠DPE的平分線上.
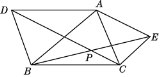
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】七(1)班同學為了解某小區家庭月均用水情況,隨機調查了該小區部分家庭,并將調查數據整理如下表(部分):
月均用 水量x/m3 | 0< x≤5 | 5< x≤10 | 10< x≤15 | 15< x≤20 | x>20 |
頻數/戶數 | 12 | 20 | 3 | ||
百分比 | 12% | 7% |
若該小區有800戶家庭,據此估計該小區月均用水量不超過10 m3的家庭有________戶.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是菱形,對角線AC與BD交于點O,且AC=80,BD=60.動點M,N分別以每秒1個單位的速度從點A,D同時出發,分別沿A→O→D和D→A運動,當點N到達點A時,M,N同時停止運動.設運動時間為t秒.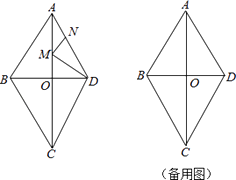
(1)求菱形ABCD的周長.
(2)設△DMN的面積為S,求S關于t的解析式,并求S的最大值(提示:需分兩種情況討論).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com