
【題目】如圖,點A、B在雙曲線y=![]() (x<0)上,連接OA、AB,以OA、AB為邊作□OABC.若點C恰落在雙曲線y=
(x<0)上,連接OA、AB,以OA、AB為邊作□OABC.若點C恰落在雙曲線y=![]() (x>0)上,此時□OABC的面積為__________.
(x>0)上,此時□OABC的面積為__________.

【答案】![]()
【解析】
如圖,過A點作AD⊥x軸于D,過C作CE⊥x軸于E,過B作BF⊥AD于F,設A(a,﹣![]() ),C(b,
),C(b,![]() ),根據△ABF≌△COE可得B(a+b,﹣
),根據△ABF≌△COE可得B(a+b,﹣![]() ),即(a+b)(﹣
),即(a+b)(﹣![]() )=﹣3,設
)=﹣3,設![]() =m,則可化方程為3m﹣
=m,則可化方程為3m﹣![]() =2,求得
=2,求得![]() =
=![]() ,
,![]() ,然后根據□OABC的面積=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)即可得解.
,然后根據□OABC的面積=2×S△OAC=2(S梯形ADEC﹣S△AOD﹣S△COE)即可得解.
解:如圖,連接AC,過A點作AD⊥x軸于D,過C作CE⊥x軸于E,過B作BF⊥AD于F,
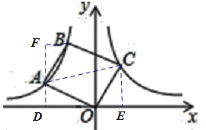
易證△ABF≌△COE,設A(a,﹣![]() ),C(b,
),C(b,![]() ),則OE=BF=b,CE=AF=
),則OE=BF=b,CE=AF=![]() ,
,
∴B(a+b,﹣![]() ),
),
∵B點在在雙曲線y=![]() (x<0)上,
(x<0)上,
∴(a+b)(﹣![]() )=﹣3,
)=﹣3,
設![]() =m,則可化方程為3m﹣
=m,則可化方程為3m﹣![]() =2,
=2,
解得m=![]() ,或m=
,或m=![]() (舍去),
(舍去),
∴![]() =
=![]() ,
,![]() ,
,
∴S□OABC=2×S△OAC
=2(S梯形ADEC﹣S△AOD﹣S△COE)
=2[![]() (﹣
(﹣![]() )(b﹣a)﹣
)(b﹣a)﹣![]() ×∣﹣3∣﹣
×∣﹣3∣﹣![]() ×2]
×2]
=﹣![]() +3+2﹣
+3+2﹣![]() ﹣5
﹣5
=![]() .
.
故答案為:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,旗桿AB的頂端B在夕陽的余輝下落在一個斜坡上的點D處,某校數學課外興趣小組的同學正在測量旗桿的高度,在旗桿的底部A處測得點D的仰角為15°,AC=10米,又測得∠BDA=45°.已知斜坡CD的坡度為i=1:![]() ,求旗桿AB的高度(
,求旗桿AB的高度(![]() ≈1.7,結果精確到個位).
≈1.7,結果精確到個位).

查看答案和解析>>
科目:初中數學 來源: 題型:
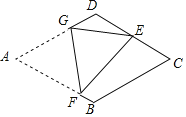
【題目】如圖,在菱形紙片ABCD中,AB=4,∠A=60°,將菱形紙片翻折,使點A落在CD的中點E處,折痕為FG,點F、G分別在邊AB、AD上.則sin∠EFG的值為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,∠A=20°.將△ABC繞點C按逆時針方向旋轉得△A′B′C,且點B在A′B′ 上,CA′ 交AB于點D,則∠BDC的度數為( )
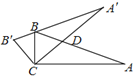
A. 40°B. 50°C. 60°D. 70°
查看答案和解析>>
科目:初中數學 來源: 題型:
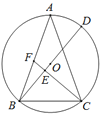
【題目】如圖,△ABC內接于⊙O,AB=AC,CF垂直直徑BD于點E,交邊AB于點F.
(1)求證:∠BFC=∠ABC.
(2)若⊙O的半徑為5,CF=6,求AF長.
查看答案和解析>>
科目:初中數學 來源: 題型:
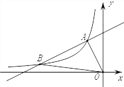
【題目】如圖,一次函數y=k1x+b的圖象與反比例函數y=![]() (x<0)的圖象相交于點A(-1,2)、點B(-4,n).
(x<0)的圖象相交于點A(-1,2)、點B(-4,n).
(1)求此一次函數和反比例函數的表達式;
(2)求△AOB的面積;
(3)在x軸上存在一點P,使△PAB的周長最小,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
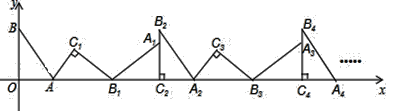
【題目】如圖,在平面直角坐標系中,將△ABO繞點A順時針旋轉到△AB1C1的位置,點B,O分別落在點B1,C1處,點B1在x軸上,再將△AB1C1繞點B1順時針旋轉到△A1B1C2的位置,點C2在x軸上,將△A1B1C2繞點C2順時針旋轉到△A2B2C2的位置,點A2在x軸上,依次進行下去….若點A(3,0),B(0,4),則點B2018的坐標為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
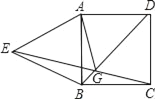
【題目】如圖所示,在正方形ABCD中,以AB為邊向正方形外作等邊三角形ABE,連接CE、BD交于點G,連接AG,那么∠AGD的底數是______度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠MON=30°,B為OM上一點,BA⊥ON于A,四邊形ABCD為正方形,P為射線BM上一動點,連結CP,將CP繞點C順時針方向旋轉90°得CE,連結BE,若AB=4,則BE的最小值為_____.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com