
【題目】如圖,在Rt△ABC中,∠ACB=90°.
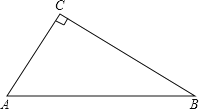
(1)利用尺規作圖,在BC邊上求作一點P,使得點P到邊AB的距離等于PC的長;(要求:尺規作圖,不寫作法,保留作圖痕跡,并把作圖痕跡用黑色簽字筆描黑)
(2)在(1)的條件下,以點P為圓心,PC長為半徑的⊙P中,⊙P與邊BC相交于點D,若AC=6,PC=3,求BD的長.
【答案】(1)如圖所示,見解析;(2)BD的長為2.
【解析】
(1)根據題意可知要作∠A的平分線,按尺規作圖的要求作角平分線即可;
(2)由切線長定理得出AC=AE,設BD=x,BE=y,則BC=6+x,BP=3+x,通過△PEB∽△ACB可得出![]() ,從而建立一個關于x,y的方程,解方程即可得到BD的長度.
,從而建立一個關于x,y的方程,解方程即可得到BD的長度.
(1)如圖所示:
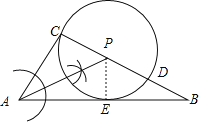
作∠A的平分線交BC于點P,
點P即為所求作的點.
(2)作PE⊥AB于點E,則PE=PC=3,
∴AB與圓相切,
∵∠ACB=90°,
∴AC與圓相切,
∴AC=AE,
設BD=x,BE=y,
則BC=6+x,BP=3+x,
∵∠B=∠B,∠PEB=∠ACB,
∴△PEB∽△ACB
∴![]()
∴![]()
解得x=2,
答:BD的長為2.


科目:初中數學 來源: 題型:
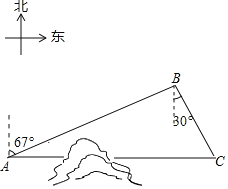
【題目】如圖,C地在A地的正東方向,因有大山阻隔,由A地到C地需要繞行B地,已知B地位于A地北偏東67°方向,距離A地520km,C地位于B地南偏東30°方向,若打通穿山隧道,建成兩地直達高鐵,求A地到C地之間高鐵線路的長(結果保留整數)(參考數據:sin67°≈0.92;cos67°≈0.38;![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
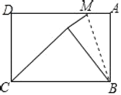
【題目】如圖,矩形紙片ABCD中,AD=5,AB=3.若M為射線AD上的一個動點,將△ABM沿BM折疊得到△NBM.若△NBC是直角三角形.則所有符合條件的M點所對應的AM長度的和為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①是由五個完全相同的小正方體組成的立體圖形,將圖①中的一個小正方體改變位置后如圖②.則三視圖發生改變的是( )

A.主視圖B.俯視圖
C.左視圖D.主視圖、俯視圖和左視圖
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰△ABC中,AB=AC=4,BC=6點D在底邊BC上,且∠DAC=∠ACD,將△ACD沿著AD所在直線翻折,使得點C落到點E處,聯結BE,那么BE的長為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,∠ADC=900,∠BAD=600,對角線AC平分∠BAD,且AB=AC=4,點E、F分別是AC、BC的中點,連接DE,EF,DF,則DF的長為_______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖二次函數的圖象與![]() 軸交于點
軸交于點![]() 和
和![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,點
,點![]() 、
、![]() 是二次函數圖象上的一對對稱點,一次函數的圖象經過
是二次函數圖象上的一對對稱點,一次函數的圖象經過![]() 、
、![]()
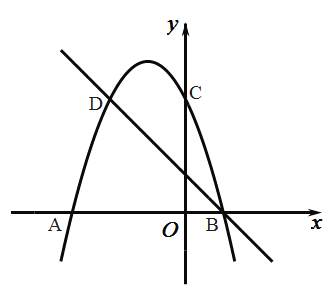
(1)求二次函數的解析式;
(2)寫出使一次函數值大于二次函數值的![]() 的取值范圍;
的取值范圍;
(3)若直線![]() 與
與![]() 軸的交點為
軸的交點為![]() 點,連結
點,連結![]() 、
、![]() ,求
,求![]() 的面積;
的面積;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在正方形ABCD中,點E、F分別在BC和CD上,AE = AF

(1)求證:BE = DF;
(2)連接AC交EF于點O,延長OC至點M,使OM = OA,連接EM、FM.判斷四邊形AEMF是什么特殊四邊形?并證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com