
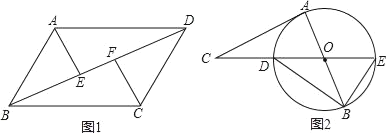
【題目】(1)已知,如圖①,在平行四邊形ABCD中,E、F是對角線BD上的兩點,且BF=DE.求證:AE=CF;
(2)已知,如圖②,AB是⊙O的直徑,CA與⊙O相切于點A.連接CO交⊙O于點D,CO的延長線交⊙O于點E.連接BE、BD,∠ABD=30°,求∠EBO和∠C的度數.
【答案】(1)詳見解析;(2)60°,30°.
【解析】
(1)先證明△BCF≌△DAE,再利用全等三角形的性質可得出:AE=CF;
(2)先求出∠EBO,再利用同弧所對的圓心角等于圓周角的2倍,可求出∠AOC,從而求出∠C的度數.
(1)證明:∵四邊形ABCD是平行四邊形,
∴AD=BC,AD∥BC.
∴∠ADE=∠FBC.
在△ADE和△CBF中,
∵AD=BC,∠ADE=∠FBC,DE=BF,
∴△ADE≌△CBF.
∴AE=CF.
(2)解:∵DE是⊙O的直徑,
∴∠DBE=90°.
∵∠ABD=30°,
∴∠EBO=∠DBE﹣∠ABD=90°﹣30°=60°.
∵AC是⊙O的切線,
∴∠CAO=90°.
又∠AOC=2∠ABD=60°,
∴∠C=180°﹣∠AOC﹣∠CAO=180°﹣60°﹣90°=30°.


科目:初中數學 來源: 題型:
【題目】如圖,已知⊙O的半徑為5,PA是⊙O的一條切線,切點為A,連接PO并延長,交⊙O于點B,過點A作AC⊥PB交⊙O于點C、交PB于點D,連接BC,當∠P=30°時,
(1)求弦AC的長;
(2)求證:BC∥PA.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,CD是⊙O的弦,且AB⊥CD于E,F為![]() 上一點,BF交CD于G,點H在CD的延長線上,且FH=GH.
上一點,BF交CD于G,點H在CD的延長線上,且FH=GH.

(1)求證:FH與⊙O相切.
(2)若FH=OA=5,FG=3![]() ,求AG的長.
,求AG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
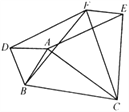
【題目】如圖,在△ABC中,AB=5,AC=12,BC=13,△ABD、△ACE、△BCF都是等邊三角形,則四邊形AEFD的面積S=__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次數學綜合實踐活動中,小明計劃測量城門大樓的高度,在點B處測得樓頂A的仰角為22°,他正對著城樓前進21米到達C處,再登上3米高的樓臺D處,并測得此時樓頂A的仰角為45°.
(1)求城門大樓的高度;
(2)每逢重大節日,城門大樓管理處都要在A,B之間拉上繩子,并在繩子上掛一些彩旗,請你求出A,B之間所掛彩旗的長度(結果保留整數).(參考數據:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新美蔬菜有限公司一年四季都有大量新鮮蔬菜銷往全國各地,已成為我區經濟發展的重要項目。近年來它的蔬菜產值不斷增加,2013年蔬菜的產值是640萬元,2015年產值達到1000萬元。
(1)求2014年、2015年蔬菜產值的年平均增長率是多少?
(2)若2016年蔬菜產值繼續穩步增長(即年增長率與前兩年的年增長率相同),那么請你估計2016年該公司的蔬菜產值將達到多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,動點D從點A出發,沿線段AC以每秒1個單位的速度向終點C運動,動點E同時從點B出發,以每秒2個單位的速度沿射線BC方向運動,當點D停止時,點E也隨之停止,連結DE,當C. D. E三點不在同一直線上時,以ED、EC我鄰邊作ECFD,設點D運動的時間為t(秒).
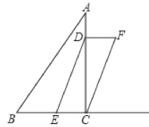
(1)用含t的代數式表示CE的長度。
(2)當F點落在△ABC的內部時,求t的取值范圍。
(3)設ECFD的面積為S(平方單位),求S與t之間的函數關系式。
(4)當點F到Rt△ABC的一條直角邊的距離是到另一條直角邊距離的2倍時,直接寫出ECFD的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com