
【題目】如圖,已知⊙O是△ABC的外接圓,AD是⊙O的直徑,且BD=BC,延長AD到E,且有∠EBD=∠CAB.
(1)求證:BE是⊙O的切線;
(2)若BC=![]() ,AC=5,求圓的直徑AD及切線BE的長.
,AC=5,求圓的直徑AD及切線BE的長.
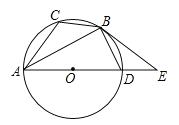
【答案】(1)證明見解析;(2)AD=6,BE=![]() .
.
【解析】
試題分析:(1)先根據(jù)等弦所對的劣弧相等,再結(jié)合∠EBD=∠CAB從而得到∠BAD=∠EBD,最后用直徑所對的圓周角為直角即可;
(2)利用三角形的中位線先求出OF,再用平行線分線段成比例定理求出半徑R,最后用切割線定理即可.
試題解析:如圖,連接OB,∵BD=BC,∴∠CAB=∠BAD,∵∠EBD=∠CAB,∴∠BAD=∠EBD,∵AD是⊙O的直徑,∴∠ABD=90°,OA=BO,∴∠BAD=∠ABO,∴∠EBD=∠ABO,∴∠OBE=∠EBD+∠OBD=∠ABD+∠OBD=∠ABD=90°,∵點B在⊙O上,∴BE是⊙O的切線;(2)如圖2,設(shè)圓的半徑為R,連接CD,∵AD為⊙O的直徑,∴∠ACCD=90°,∵BC=BD,∴OB⊥CD,∴OB∥AC,∵OA=OD,∴OF=![]() AC=
AC=![]() ,∵四邊形ACBD是圓內(nèi)接四邊形,∴∠BDE=∠ACB,∵∠DBE=∠ACB,∴△DBE∽△CAB,∴
,∵四邊形ACBD是圓內(nèi)接四邊形,∴∠BDE=∠ACB,∵∠DBE=∠ACB,∴△DBE∽△CAB,∴![]() ,∴
,∴![]() ,∴DE=
,∴DE=![]() ,∵∠OBE=∠OFD=90°,∴DF∥BE,∴
,∵∠OBE=∠OFD=90°,∴DF∥BE,∴![]() ,∴
,∴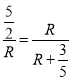 ,∵R>0,∴R=3,∴直徑AD=6.∵BE是⊙O的切線,∴BE=
,∵R>0,∴R=3,∴直徑AD=6.∵BE是⊙O的切線,∴BE=![]() =
=![]() =
=![]() .
.



科目:初中數(shù)學(xué) 來源: 題型:
【題目】在開展“學(xué)雷鋒社會實踐”活動中,某校為了解全校1200名學(xué)生參加活動的情況,隨機調(diào)查了50名學(xué)生每人參加活動的次數(shù),并根據(jù)數(shù)據(jù)繪成條形統(tǒng)計圖如圖. 
(Ⅰ)求這50個樣本數(shù)據(jù)的平均數(shù)、眾數(shù)和中位數(shù);
(Ⅱ)根據(jù)樣本數(shù)據(jù),估算該校1200名學(xué)生共參加了多少次活動?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
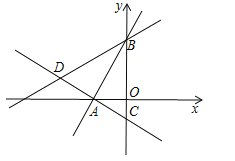
【題目】如圖所示,在平面直角坐標(biāo)系中,過點A(![]() ,0)的兩條直線分別交y軸于B、C兩點,且B、C兩點的縱坐標(biāo)分別是一元二次方程
,0)的兩條直線分別交y軸于B、C兩點,且B、C兩點的縱坐標(biāo)分別是一元二次方程![]() 的兩個根.
的兩個根.
(1)求線段BC的長度;
(2)試問:直線AC與直線AB是否垂直?請說明理由;
(3)若點D在直線AC上,且DB=DC,求點D的坐標(biāo);
(4)在(3)的條件下,直線BD上是否存在點P,使以A、B、P三點為頂點的三角形是等腰三角形?若存在,請直接寫出P點的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】請從下列三類試題中選答一題,
(1)小新出生時父親28歲,現(xiàn)在父親的年齡是小新的3倍,求現(xiàn)在小新的年齡.
(2)兩輛汽車從相距240 ![]() 的兩地同時出發(fā)相向而行,甲車的速度比乙車的速度的2倍慢20
的兩地同時出發(fā)相向而行,甲車的速度比乙車的速度的2倍慢20 ![]() ,1.5h后兩車相遇,兩車的速度各是多少?
,1.5h后兩車相遇,兩車的速度各是多少?
(3)用A4紙在某譽印社復(fù)印文件,復(fù)印頁數(shù)不超過20頁時,每頁收費0.12元;復(fù)印頁數(shù)超過20頁時,超過部分每頁收費0.09元,在圖書館復(fù)印同樣的文件,每頁收費0.1元.復(fù)印張數(shù)為多少時,兩處收費相同?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】我們知道,無限循環(huán)小數(shù)都可以轉(zhuǎn)化為分?jǐn)?shù).例如:將 ![]() 轉(zhuǎn)化為分?jǐn)?shù)時,可設(shè)
轉(zhuǎn)化為分?jǐn)?shù)時,可設(shè) ![]() =x,則x=0.3+
=x,則x=0.3+ ![]() x,解得x=
x,解得x= ![]() ,即
,即 ![]() =
= ![]() .仿此方法,將
.仿此方法,將 ![]() 化成分?jǐn)?shù)是 .
化成分?jǐn)?shù)是 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】A(0,4)是直角坐標(biāo)系y軸上一點,P是x軸上一動點,從原點O出發(fā),沿正半軸運動,速度為每秒1個單位長度,以P為直角頂點在第一象限內(nèi)作等腰Rt△APB.設(shè)P點的運動時間為t秒.
(1)若AB∥x軸,求t的值;
(2)設(shè)點B的坐標(biāo)為(x,y),試求y關(guān)于x的函數(shù)表達(dá)式;
(3)當(dāng)t=3時,平面直角坐標(biāo)系內(nèi)有一點M(3,a),請直接寫出使△APM為等腰三角形的點M的坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com