
【題目】已知:P是正方形ABCD對角線AC上一點,PE⊥AB,PF⊥BC,E、F分別為垂足.
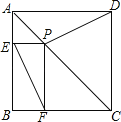
(1)求證:DP=EF.
(2)試判斷DP與EF的位置關系并說明理由.
【答案】見解析
【解析】
試題分析:(1)連結PB,由正方形的性質得到BC=DC,∠BCP=∠DCP,接下來證明△CBP≌△CDP,于是得到DP=BP,然后證明四邊形BFPE是矩形,由矩形的對角線相等可得到BP=EF,從而等量代換可證得問題的答案;
(2)延長DP交EF于G,延長EP交CD于H,連接PB.由(1)可知△CBP≌△CDP,依據全等三角形對應角相等可得到∠CDP=∠CBP,由四邊形EPFB是矩形可證明∠CBP=∠FEP,從而得到∠HDP=∠FEP,由∠DPH+∠PDH=90°可證明∠EPG+∠PEG=90°,從而可得到問題答案.
證明:(1)如圖1所示:連結PB.
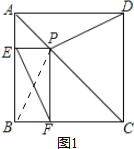
∵四邊形ABCD是正方形,
∴BC=DC,∠BCP=∠DCP=45°.
∵在△CBP和△CDP中,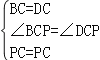 ,
,
∴△CBP≌△CDP.
∴DP=BP.
∵PE⊥AB,PF⊥BC,∠B=90°
∴四邊形BFPE是矩形.
∴BP=EF.
∴DP=EF.
(2)DP⊥EF.
理由:如圖2所示:延長DP交EF于G,延長EP交CD于H,連接PB.
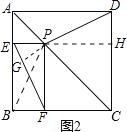
∵△CBP≌△CDP,
∴∠CDP=∠CBP.
∵四邊形BFPE是矩形,
∴∠CBP=∠FEP.
∴∠CDP=∠FEP.
又∵∠EPG=∠DPH.
∴∠EGP=∠DHP.
∵PE⊥AB,AB∥DC
∴PH⊥DC.即∠DHP=90°.
∴∠EGP=∠DHP=90°
∴PG⊥EF,即DP⊥EF.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案 全優沖刺100分系列答案
全優沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】某車間有26名工人,每人每天可以生產800個螺釘或1000個螺母,1個螺釘需要配2個螺母,為使每天生產的螺釘和螺母剛好配套.設安排x名工人生產螺釘,則下面所列方程正確的是( )
A.2×1000(26﹣x)=800x B.1000(13﹣x)=800x
C.1000(26﹣x)=2×800x D.1000(26﹣x)=800x
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△BAD是由△BEC在平面內繞點B旋轉60°而得,且AB⊥BC,BE=CE,連接DE.
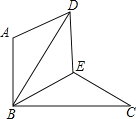
(1)求證:△BDE≌△BCE;
(2)試判斷四邊形ABED的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2016年5月22日10時5分,西藏日咯則市定日縣發生5.3級地震,該縣部分地區受災嚴重,我解放軍某部火速向災區救援,最初坐車以某一速度勻速前進,中途由于道路出現泥石流,被阻停下,耽誤了一段時間,為了盡快趕到災區救援,官兵們下車急行軍勻速步行前往,下列是官兵們離出發地的距離S(千米)與行進時間t(小時)的函數大致圖象,你認為正確的是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB的垂直平分線MN交AB于點E,交AC于點D,且AC=15cm,△BCD的周長等于25cm.

(1)求BC的長;
(2)若∠A=36°,并且AB=AC,求證:BC=BD.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一副直角三角板疊放如圖所示,現將含45°角的三角板ADE固定不動,把含30°角的三角板ABC繞頂點A順時針旋轉∠α(α=∠BAD且0°<α<180°),使兩塊三角板至少有一組邊平行.
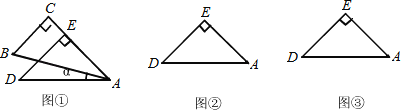
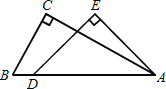
(1)如圖①,α= °時,BC∥DE;
(2)請你分別在圖②、圖③的指定框內,各畫一種符合要求的圖形,標出α,并完成各項填空:圖②中α= °時, ∥ ;圖③中α= °時, ∥ .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com