
【題目】已知,Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,點P是AB上一點,連接CP,將∠B沿CP折疊,使點B落在B'處.以下結論正確的有________
①當AB'⊥AC時,AB'的長為![]() ;
;
②當點P位于AB中點時,四邊形ACPB'為菱形;
③當∠B'PA=30°時,![]() ;
;
④當CP⊥AB時,AP:AB':BP=1:2:3.
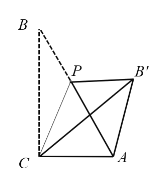
【答案】①②④
【解析】
由折疊的性質及直角三角形的性質對結論一一判斷即可.
解:①AC=1,∠B=30°可知BC=![]() ,由翻折可知:B′C=BC=
,由翻折可知:B′C=BC=![]() ,
,
因為AB'⊥AC,由勾股定理可知:
AB'=![]() =
=![]() ,正確.
,正確.
②當點P位于AB中點時,CP=PB=PA=AC=PB′,∠B'PA=PAC=60°,PB'∥AC,
所以四邊形ACPB'是平行四邊形,
又PC=AC,
所以四邊形ACPB'是菱形,正確.
③當∠B'PA=30°時,可知四邊形BCB′P是菱形,BP=BC=![]() ;AP=2-
;AP=2-![]() ,
,
![]() 成立,故不正確.
成立,故不正確.
④當CP⊥AB時,∠B'=∠B'CA=30°,AC=AB',∠ACP=∠B=30°,
設AP=a,則AB'=AC=2a;AB=4a,PB=3a;
所以:AP:AB':BP=a:2a:3a=1:2:3,正確.
故答案為:①②④.


 教學練新同步練習系列答案
教學練新同步練習系列答案 課前課后同步練習系列答案
課前課后同步練習系列答案 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案科目:初中數學 來源: 題型:
【題目】如圖1,已知正方形ABCD,E是線段BC上一點,N是線段BC延長線上一點,以AE為邊在直線BC的上方作正方形AEFG.
(1)連接GD,求證![]() ;
;
(2)連接FC,求![]() 的值;
的值;
(3)如圖2,將圖1中正方形ABCD改為矩形ABCD,![]() ,
,![]() ,E是線段BC上一動點(不含端點B,C),以AE為邊在直線BC的上方作矩形AEFG,使頂點G恰好落在射線CD上.當點E由B向C運動時,判斷
,E是線段BC上一動點(不含端點B,C),以AE為邊在直線BC的上方作矩形AEFG,使頂點G恰好落在射線CD上.當點E由B向C運動時,判斷![]() 的值是否為定值?若是,求出該定值;若不是,請說明理由.
的值是否為定值?若是,求出該定值;若不是,請說明理由.
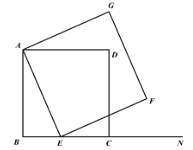
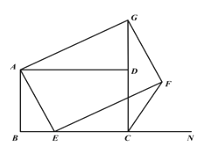
圖1 圖2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解網課學習的整體效果,啟智中學讓學生參與了關于網課學習滿意度的調查,將全校![]() 名學生的調查結果制成如圖所示的扇形統計圖,下列說法錯誤的是( )
名學生的調查結果制成如圖所示的扇形統計圖,下列說法錯誤的是( )
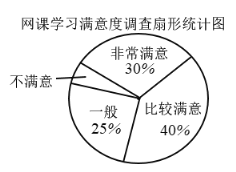
A.覺得“比較滿意”的學生人數最多
B.覺得“一般”的學生有![]() 人
人
C.覺得“不滿意”的學生人數對應的扇形圓心角度數是![]()
D.覺得“非常滿意”的人數是“不滿意”人數的![]() 倍
倍
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() 、
、![]() ,動點
,動點![]() 以每秒2個單位長度的速度從點
以每秒2個單位長度的速度從點![]() 向終點
向終點![]() 運動,過點
運動,過點![]() 作
作![]() ,交直線
,交直線![]() 于點
于點![]() .設
.設![]() ,將
,將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 得到線段
得到線段![]() ,連接
,連接![]() .設四邊形
.設四邊形![]() 與
與![]() 的重疊部分面積為
的重疊部分面積為![]() (平方單位),
(平方單位),![]() ,點
,點![]() 的運動時間為
的運動時間為![]() 秒.
秒.

(1)求![]() 的長;
的長;
(2)求證:四邊形![]() 是平行四邊形;
是平行四邊形;
(3)求![]() 與
與![]() 的函數關系式,并直接寫出自變量取值范圍.
的函數關系式,并直接寫出自變量取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】放風箏是大家喜愛的一種運動,星期天的上午小明在市政府廣場上放風箏.如圖,他在A處不小心讓風箏掛在了一棵樹梢上,風箏固定在了D處,此時風箏線AD與水平線的夾角為30°,為了便于觀察,小明迅速向前邊移動,收線到達了離A處10米的B處,此時風箏線BD與水平線的夾角為45°.已知點A,B,C在同一條水平直線上,請你求出小明此時所收回的風箏線的長度是多少米?(風箏線AD,BD均為線段,![]() ≈1.414,
≈1.414,![]() ≈1.732,最后結果精確到1米).
≈1.732,最后結果精確到1米).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】王老師從本校九年級質量檢測的成績中隨機地抽取一些同學的數學成績做質量分析,他先按照等級繪制這些人數學成績的扇形統計圖,如圖(1)所示,數學成績等級標準見表1,又按分數段繪制成績分布表,如表2,
表1
等級 | 分數x的范圍 |
A | a≤x≤100 |
B | 80≤x<a |
C | 60≤x<80 |
D | 0≤x<60 |
表2
分數段 | x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
人數 | 5 | 10 | m | 12 | n |
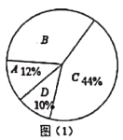
分數段為90≤x≤100的n個人中,其成績的中位數是95分.
根據以上信息回答下面問題:
(1)王老師抽查了多少人?m、n的值分別是多少;
(2)小明在此考試中得了95分,他說自己在這些考試中數學成績是A等級,他說的對嗎?為什么?
(3)若此次測試數學學科普高的預測線是70分,該校九年級有900名學生,求數學學科達到普高預測線的學生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解學生課外閱讀情況,就學生每周閱讀時間隨機調查了部分學生,調查結果按性別整理如下:
女生閱讀時間人數統計表
閱讀時間 | 人數 | 占女生人數百分比 |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
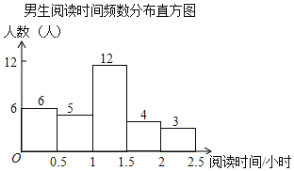
根據圖表解答下列問題:
(1)在女生閱讀時間人數統計表中,![]() ,
,![]() ;
;
(2)此次抽樣調查中,共抽取了 名學生,學生閱讀時間的中位數在 時間段;
(3)從閱讀時間在2~2.5小時的5名學生中隨機抽取2名學生參加市級閱讀活動,恰好抽到男女生各一名的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學課上,王老師畫好圖后并出示如下內容:“己知:![]() 為
為![]() 的直徑,
的直徑,![]() 過
過![]() 的中點
的中點![]() ,
,![]() 為
為![]() 的切線.”
的切線.”
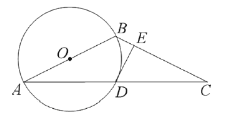
(1)王老師要求同學們根據己知條件,在不添加線段與標注字母的前提下,寫出三個正確的結論,并選擇其中一個加以證明.
(2)王老師說:如果添加條件“![]() ,
,![]() ”,則能求出
”,則能求出![]() 的直徑.請你寫出求解過程,
的直徑.請你寫出求解過程,
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩所學校選派相同人數的老師參加志愿者活動,參加活動時長分別被制成下列兩個統計圖,根據以上信息,整理分析數據如下表:
平均時間/小時 | 中位數/小時 | 眾數/小時 | 方差/小時 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
![]() 求出表格中
求出表格中![]() 的值.
的值.
![]() 分別運用表中的統計量,簡要分析這兩所學校參加志愿者活動的時長,若選其中一所學校作為志愿推廣學校,你認為應該選哪所?
分別運用表中的統計量,簡要分析這兩所學校參加志愿者活動的時長,若選其中一所學校作為志愿推廣學校,你認為應該選哪所?
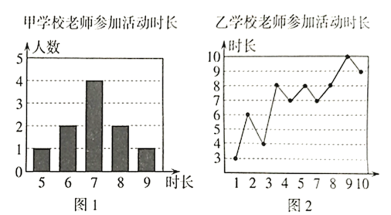
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com