
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,對稱軸為x=1,給出下列結論:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正確的結論有( )
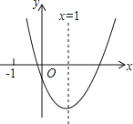
A. 1個 B. 2個 C. 3個 D. 4個
 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案科目:初中數學 來源: 題型:
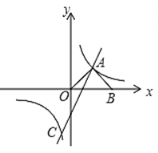
【題目】如圖,在平面直角坐標系中,直線![]() 與雙曲線
與雙曲線![]() 交于A、C兩點,
交于A、C兩點,![]() 交x軸于點B,且OA=AB.
交x軸于點B,且OA=AB.
(1)求雙曲線的解析式;
(2)求點C的坐標,并直接寫出![]() 時x的取值范圍;
時x的取值范圍;
(3)設AC直線與y軸交于點D,求D點到OA的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有一張矩形紙片,長10cm,寬6cm,在它的四角各減去一個同樣的小正方形,然后折疊成一個無蓋的長方體紙盒.若紙盒的底面(圖中陰影部分)面積是32cm2,求剪去的小正方形的邊長.設剪去的小正方形邊長是xcm,根據題意可列方程為( )

A. 10×6﹣4×6x=32 B. (10﹣2x)(6﹣2x)=32
C. (10﹣x)(6﹣x)=32 D. 10×6﹣4x2=32
查看答案和解析>>
科目:初中數學 來源: 題型:
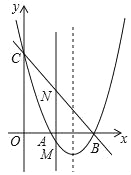
【題目】如圖,拋物線y=x2+bx+c與x軸交于點A和B(3,0),與y軸交于點C(0,3).
(1)求拋物線的解析式;
(2)若點M是拋物線上在x軸下方的動點,過M作MN∥y軸交直線BC于點N,求線段MN的最大值;
(3)E是拋物線對稱軸上一點,F是拋物線上一點,是否存在以A,B,E,F為頂點的四邊形是平行四邊形?若存在,請直接寫出點F的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O的直徑AB=4cm,點C為線段AB上一動點,過點C作AB的垂線交⊙O于點D,E,連結AD,AE.設AC的長為xcm,△ADE的面積為ycm2.
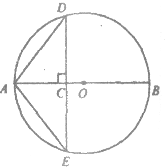
小東根據學習函數的經驗,對函數y隨自變量x的變化而變化的規律進行了探究.
下面是小東的探究過程,請補充完整:
(1)通過取點、畫圖、測量、分析,得到了y與x的幾組對應值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm2 | 0 | 0.7 | 1.7 | 2.9 | 4.8 | 5.2 | 4.6 | 0 |
(2)如圖,建立平面直角坐標系![]() ,描出以補全后的表中各對對應值為坐標的點,畫出該函數的圖象;
,描出以補全后的表中各對對應值為坐標的點,畫出該函數的圖象;

(3)結合畫出的函數圖象,解決問題:當△ADE的面積為4cm2時,AC的長度約為___________cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD中,AB=2,∠B=120°,點M是AD的中點,點P由點A出發,沿A→B→C→D作勻速運動,到達點D停止,則△APM的面積y與點P經過的路程x之間的函數關系的圖象大致是( )
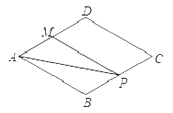
A. 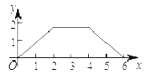 B.
B. 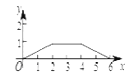 C.
C. 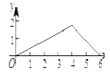 D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,點D是AB邊的中點,過D作DE⊥BC于點E,點P是邊BC上的一個動點,AP與CD相交于點Q.當AP+PD的值最小時,AQ與PQ之間的數量關系是( )

A.AQ= PQ B.AQ=3PQ C.AQ=![]() PQ D.AQ=4PQ
PQ D.AQ=4PQ
查看答案和解析>>
科目:初中數學 來源: 題型:
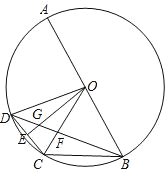
【題目】如圖,AB是⊙O的直徑,弦BC=OB,點D是![]() 上一動點,點E是CD中點,連接BD分別交OC,OE于點F,G.
上一動點,點E是CD中點,連接BD分別交OC,OE于點F,G.
(1)求∠DGE的度數;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)記△CFB,△DGO的面積分別為S1,S2,若![]() =k,求
=k,求![]() 的值.(用含k的式子表示)
的值.(用含k的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
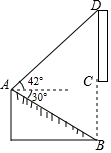
【題目】小婷在放學路上,看到隧道上方有一塊宣傳“中國﹣南亞博覽會”的豎直標語牌CD.她在A點測得標語牌頂端D處的仰角為42°,測得隧道底端B處的俯角為30°(B,C,D在同一條直線上),AB=10m,隧道高6.5m(即BC=65m),求標語牌CD的長(結果保留小數點后一位).(參考數據:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com