
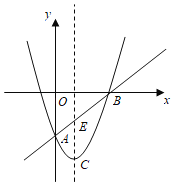
【題目】如圖,在平面直角坐標(biāo)系![]() 中,已知拋物線
中,已知拋物線![]() 與直線
與直線![]() 都經(jīng)過
都經(jīng)過![]() 、
、![]() 兩點(diǎn),該拋物線的頂點(diǎn)為C.
兩點(diǎn),該拋物線的頂點(diǎn)為C.
(1)求此拋物線和直線![]() 的解析式;
的解析式;
(2)設(shè)直線![]() 與該拋物線的對稱軸交于點(diǎn)E,在射線
與該拋物線的對稱軸交于點(diǎn)E,在射線![]() 上是否存在一點(diǎn)M,過M作x軸的垂線交拋物線于點(diǎn)N,使點(diǎn)M、N、C、E是平行四邊形的四個頂點(diǎn)?若存在,求點(diǎn)M的坐標(biāo);若不存在,請說明理由;
上是否存在一點(diǎn)M,過M作x軸的垂線交拋物線于點(diǎn)N,使點(diǎn)M、N、C、E是平行四邊形的四個頂點(diǎn)?若存在,求點(diǎn)M的坐標(biāo);若不存在,請說明理由;
(3)設(shè)點(diǎn)P是直線![]() 下方拋物線上的一動點(diǎn),當(dāng)
下方拋物線上的一動點(diǎn),當(dāng)![]() 面積最大時,求點(diǎn)P的坐標(biāo),并求
面積最大時,求點(diǎn)P的坐標(biāo),并求![]() 面積的最大值.
面積的最大值.
【答案】(1)拋物線的解析式為![]() ,直線
,直線![]() 的解析式為
的解析式為![]() ,(2)
,(2)![]() 或
或![]() .(3)當(dāng)
.(3)當(dāng)![]() 時,
時,![]() 面積的最大值是
面積的最大值是![]() ,此時P點(diǎn)坐標(biāo)為
,此時P點(diǎn)坐標(biāo)為![]() .
.
【解析】
(1)將![]() 、
、![]() 兩點(diǎn)坐標(biāo)分別代入二次函數(shù)的解析式和一次函數(shù)解析式即可求解;
兩點(diǎn)坐標(biāo)分別代入二次函數(shù)的解析式和一次函數(shù)解析式即可求解;
(2)先求出C點(diǎn)坐標(biāo)和E點(diǎn)坐標(biāo),則![]() ,分兩種情況討論:①若點(diǎn)M在x軸下方,四邊形
,分兩種情況討論:①若點(diǎn)M在x軸下方,四邊形![]() 為平行四邊形,則
為平行四邊形,則![]() ,②若點(diǎn)M在x軸上方,四邊形
,②若點(diǎn)M在x軸上方,四邊形![]() 為平行四邊形,則
為平行四邊形,則![]() ,設(shè)
,設(shè)![]() ,則
,則![]() ,可分別得到方程求出點(diǎn)M的坐標(biāo);
,可分別得到方程求出點(diǎn)M的坐標(biāo);
(3)如圖,作![]() 軸交直線
軸交直線![]() 于點(diǎn)G,設(shè)
于點(diǎn)G,設(shè)![]() ,則
,則![]() ,可由
,可由![]() ,得到m的表達(dá)式,利用二次函數(shù)求最值問題配方即可.
,得到m的表達(dá)式,利用二次函數(shù)求最值問題配方即可.
解:(1)∵拋物線![]() 經(jīng)過
經(jīng)過![]() 、
、![]() 兩點(diǎn),
兩點(diǎn),
∴![]() ,
,
∴![]() ,
,
∴拋物線的解析式為![]() ,
,
∵直線![]() 經(jīng)過
經(jīng)過![]() 、
、![]() 兩點(diǎn),
兩點(diǎn),
∴![]() ,解得:
,解得:![]() ,
,
∴直線![]() 的解析式為
的解析式為![]() ,
,
(2)∵![]() ,
,
∴拋物線的頂點(diǎn)C的坐標(biāo)為![]() ,
,
∵![]() 軸,
軸,
∴![]() ,
,
∴![]() ,
,
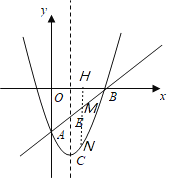
①如圖,若點(diǎn)M在x軸下方,四邊形![]() 為平行四邊形,則
為平行四邊形,則![]() ,
,
設(shè)![]() ,則
,則![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
∴![]() ,
,
②如圖,若點(diǎn)M在x軸上方,四邊形![]() 為平行四邊形,則
為平行四邊形,則![]() ,
,

設(shè)![]() ,則
,則![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
∴![]() ,
,
綜合可得M點(diǎn)的坐標(biāo)為![]() 或
或![]() .
.
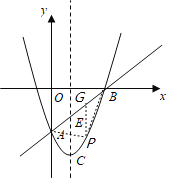
(3)如圖,作![]() 軸交直線
軸交直線![]() 于點(diǎn)G,
于點(diǎn)G,
設(shè)![]() ,則
,則![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴當(dāng)![]() 時,
時,![]() 面積的最大值是
面積的最大值是![]() ,此時P點(diǎn)坐標(biāo)為
,此時P點(diǎn)坐標(biāo)為![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀對學(xué)生的成長有著深遠(yuǎn)的影響.某中學(xué)為了解學(xué)生每周課余閱讀的時間,在本校隨機(jī)抽取若干名學(xué)生進(jìn)行調(diào)查,并依據(jù)調(diào)查結(jié)果經(jīng)制了以下不完整的統(tǒng)計圖表.
組別 | 時間(小時) | 頻數(shù)(人數(shù)) | 頻率 |
A |
| 6 |
|
B |
|
|
|
C |
| 10 |
|
D |
| 8 |
|
E |
| 4 |
|
合計 | 1 |
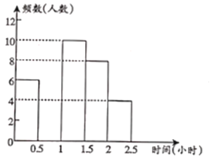
請根據(jù)圖表中的信息,解答下列問題:
(1)表中的![]() ,
,![]() ,將頻數(shù)分布直方圖補(bǔ)全;
,將頻數(shù)分布直方圖補(bǔ)全;
(2)估計該校2000名學(xué)生中,每周課余閱讀時間不足1小時的學(xué)生大約有多少名?
(3)![]() 組的4人中,有1名男生和3名女生,該校計劃在
組的4人中,有1名男生和3名女生,該校計劃在![]() 組學(xué)生中隨機(jī)選出兩人向全校同學(xué)作讀書心得報告,求抽取的兩名學(xué)生剛好是1名男生和1名女生的概率.
組學(xué)生中隨機(jī)選出兩人向全校同學(xué)作讀書心得報告,求抽取的兩名學(xué)生剛好是1名男生和1名女生的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知⊙O的半徑是2,點(diǎn)A,B在⊙O上,且∠AOB=90°,動點(diǎn)C在⊙O上運(yùn)動(不與A,B重合),點(diǎn)D為線段BC的中點(diǎn),連接AD,則線段AD的長度最大值是_______.
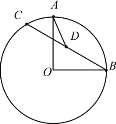
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△OAB中,∠AOB=90°,AO=2,BO=4.將△OAB繞頂點(diǎn)O按順時針方向旋轉(zhuǎn)到△OA1B1處,此時線段OB1與AB的交點(diǎn)D恰好為線段AB的中點(diǎn),線段A1B1與OA交于點(diǎn)E,則圖中陰影部分的面積__.
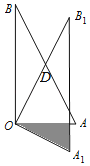
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,拋物線y=x2+bx+c經(jīng)過A、B兩點(diǎn),A、B兩點(diǎn)的坐標(biāo)分別為(﹣1,0)、(0,﹣3).
(1)求拋物線的函數(shù)解析式;
(2)點(diǎn)E為拋物線的頂點(diǎn),點(diǎn)C為拋物線與x軸的另一交點(diǎn),點(diǎn)D為y軸上一點(diǎn),且DC=DE,求出點(diǎn)D的坐標(biāo);
(3)在第二問的條件下,在直線DE上存在點(diǎn)P,使得以C、D、P為頂點(diǎn)的三角形與△DOC相似,請你直接寫出所有滿足條件的點(diǎn)P的坐標(biāo).
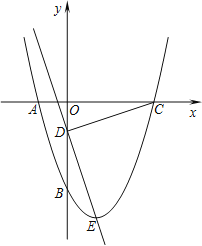
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 過點(diǎn)A(m-2,n), B(m+4,n),C(m,
過點(diǎn)A(m-2,n), B(m+4,n),C(m,![]() ).
).
(1)b=__________(用含m的代數(shù)式表示);
(2)求△ABC的面積;
(3)當(dāng)![]() 時,均有
時,均有![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,二次函數(shù)![]() 的圖像與
的圖像與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,
,![]() (
(![]() 在
在![]() 左側(cè)),與
左側(cè)),與![]() 軸正半軸交于點(diǎn)
軸正半軸交于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 在拋物線上,
在拋物線上,![]() 軸,且
軸,且![]() .
.
(1)求點(diǎn)![]() ,
,![]() 的坐標(biāo)及
的坐標(biāo)及![]() 的值;
的值;
(2)點(diǎn)![]() 為
為![]() 軸右側(cè)拋物線上一點(diǎn).
軸右側(cè)拋物線上一點(diǎn).
①如圖①,若![]() 平分
平分![]() ,
,![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,求點(diǎn)
,求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
②如圖②,拋物線上一點(diǎn)![]() 的橫坐標(biāo)為2,直線
的橫坐標(biāo)為2,直線![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作直線
作直線![]() 的垂線,垂足為
的垂線,垂足為![]() ,若
,若![]() ,求點(diǎn)
,求點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
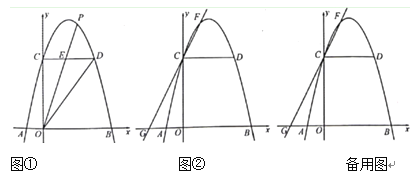
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知二次函數(shù)![]() 的圖象與
的圖象與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() 、
、![]() ,與
,與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .
.
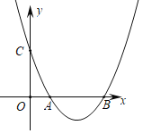
(1)求二次函數(shù)的解析式;
(2)若點(diǎn)![]() 為拋物線上的一點(diǎn),點(diǎn)
為拋物線上的一點(diǎn),點(diǎn)![]() 為對稱軸上的一點(diǎn),且以點(diǎn)
為對稱軸上的一點(diǎn),且以點(diǎn)![]() 、
、![]() 、
、![]() 、
、![]() 為頂點(diǎn)的四邊形為平行四邊形,求點(diǎn)
為頂點(diǎn)的四邊形為平行四邊形,求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(3)點(diǎn)![]() 是二次函數(shù)第四象限圖象上一點(diǎn),過點(diǎn)
是二次函數(shù)第四象限圖象上一點(diǎn),過點(diǎn)![]() 作
作![]() 軸的垂線,交直線
軸的垂線,交直線![]() 于點(diǎn)
于點(diǎn)![]() ,求四邊形
,求四邊形![]() 面積的最大值及此時點(diǎn)
面積的最大值及此時點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】近幾年,中學(xué)生過生日互送禮物甚至有部分家長為慶賀孩子生日大擺宴席攀比之風(fēng)已成為社會關(guān)注熱點(diǎn).為此某媒體記者就中學(xué)生攀比心理的成因?qū)δ呈谐菂^(qū)若干名市民進(jìn)行了調(diào)查,調(diào)查結(jié)果分為四組:![]() 社會環(huán)境的影響;
社會環(huán)境的影響;![]() 學(xué)校正確引導(dǎo)的缺失;
學(xué)校正確引導(dǎo)的缺失;![]() 家長榜樣示范的不足;
家長榜樣示范的不足;![]() 其他.并將調(diào)查結(jié)果繪制成如下條形統(tǒng)計圖和扇形統(tǒng)計圖
其他.并將調(diào)查結(jié)果繪制成如下條形統(tǒng)計圖和扇形統(tǒng)計圖![]() 均不完整
均不完整![]()
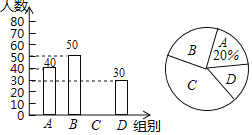
請根據(jù)圖中提供的信息,解答下列問題:
![]() 扇形統(tǒng)計圖中,B組所在扇形的圓心角度數(shù)是______;
扇形統(tǒng)計圖中,B組所在扇形的圓心角度數(shù)是______;
![]() 將條形統(tǒng)計圖補(bǔ)充完整;
將條形統(tǒng)計圖補(bǔ)充完整;
![]() 根據(jù)抽樣調(diào)查結(jié)果,請你估計該市城區(qū)120000名市民中有多少名市民持C組觀點(diǎn);
根據(jù)抽樣調(diào)查結(jié)果,請你估計該市城區(qū)120000名市民中有多少名市民持C組觀點(diǎn);
![]() 針對現(xiàn)在部分同學(xué)因舉行生日宴會而造成極大浪費(fèi)的現(xiàn)象,請你簡單說說中學(xué)生大操大辦慶祝生日的危害性,并提出合理化的建議.
針對現(xiàn)在部分同學(xué)因舉行生日宴會而造成極大浪費(fèi)的現(xiàn)象,請你簡單說說中學(xué)生大操大辦慶祝生日的危害性,并提出合理化的建議.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com