
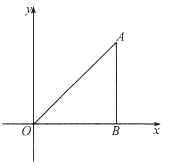
【題目】如圖,將一個直角三角形紙片![]() ,放置在平面直角坐標系中,點
,放置在平面直角坐標系中,點![]() ,點
,點![]() ,點
,點![]() .將
.將![]() 沿
沿![]() 翻折得到
翻折得到![]() (點
(點![]() 為點
為點![]() 的對應點).
的對應點).
(Ⅰ)求![]() 的長及點
的長及點![]() 的坐標;
的坐標;
(Ⅱ)點![]() 是線段
是線段![]() 上的點,點
上的點,點![]() 是線段
是線段![]() 上的點.
上的點.
①已知![]() ,
,![]() ,
,![]() 是
是![]() 軸上的動點,當
軸上的動點,當![]() 取最小值時,求出點
取最小值時,求出點![]() 的坐標及點
的坐標及點![]() 到直線
到直線![]() 的距離;
的距離;
②連接![]() ,
,![]() ,且
,且![]() ,現(xiàn)將
,現(xiàn)將![]() 沿
沿![]() 翻折得到
翻折得到![]() (點
(點![]() 為點
為點![]() 的對應點),再將
的對應點),再將![]() 繞點
繞點![]() 順時針旋轉,旋轉過程中,射線
順時針旋轉,旋轉過程中,射線![]() ,
,![]() 交直線
交直線![]() 分別為點
分別為點![]() ,
,![]() ,最后將
,最后將![]() 沿
沿![]() 翻折得到
翻折得到![]() (點
(點![]() 為點
為點![]() 的對應點),連接
的對應點),連接![]() ,若
,若![]() ,求點
,求點![]() 的坐標(直接寫出結果即可).
的坐標(直接寫出結果即可).
【答案】(Ⅰ)![]() ,
,![]() 點坐標為
點坐標為![]() ;(Ⅱ)①點
;(Ⅱ)①點![]() 的坐標為
的坐標為![]() ,點
,點![]() 到直線
到直線![]() 的距離為
的距離為![]() ;②
;②![]() 或
或![]() 或
或![]() .
.
【解析】
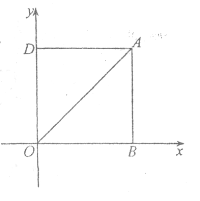
(Ⅰ)根據(jù)A點坐標和翻折的性質可得四邊形OBAD為正方形,即可得出D點坐標,再利用勾股定理得出OA的長.
(Ⅱ)①作點![]() 關于
關于![]() 軸的對稱點
軸的對稱點![]() ,連接
,連接![]() 與
與![]() 軸交于點
軸交于點![]() ,則點
,則點![]() 即為所求,再根據(jù)待定系數(shù)法確定直線
即為所求,再根據(jù)待定系數(shù)法確定直線![]() 的解析式,求出直線
的解析式,求出直線![]() 與x軸的交點
與x軸的交點![]() 的坐標,再根據(jù)等積法求出點
的坐標,再根據(jù)等積法求出點![]() 到直線
到直線![]() 的距離即可.
的距離即可.
②分(a)當點M在線段EA的延長線上,點N在線段AE時,(b)當點M,N在線段EA上時,(c)當點M在線段EA上,點N在AE的延長線上時,三種情況進行討論,作MH⊥OB于H,GK⊥EB于K,然后證明△AMH≌△GAK,推出HM=EH=BK,BH=GK,所以BH=EK=GK,從而得出∠MEG=90°,由NE:EG=5:12,設NE=5k,EG=12k,則MN=NG=13k,EM=18k,可得BH=GK=EK=6![]() k,EH=MH=9
k,EH=MH=9![]() k,再根據(jù)HE=AH+AE,得出關于k的方程,得出k的值即可解決問題;
k,再根據(jù)HE=AH+AE,得出關于k的方程,得出k的值即可解決問題;
解:(Ⅰ)如圖,∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() .
.
∵![]() ,
,
∴![]() .
.
∵將![]() 沿
沿![]() 翻折得到
翻折得到![]() ,
,
∴![]() .
.
∴![]()
∴點![]() 落在
落在![]() 軸上.
軸上.![]() 點坐標為
點坐標為![]() .
.
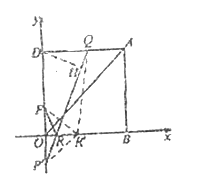
(Ⅱ)①如圖,作點![]() 關于
關于![]() 軸的對稱點
軸的對稱點![]() ,連接
,連接![]() 與
與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() ,若在
,若在![]() 軸上任取點
軸上任取點![]() (與點
(與點![]() 不重合).連接
不重合).連接![]() ,
,![]() ,
,![]() ,
,
由![]() ,
,
可知![]() 最小.
最小.
∵將![]() 沿
沿![]() 翻折得到
翻折得到![]() .
.
∴![]() ,
,![]()
∵![]() ,
,
![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
設直線![]() 的方程為
的方程為![]() .
.
將![]() 的坐標代入,
的坐標代入,
得![]() ,
,
解得![]() .
.
∴直線![]() 的方程為
的方程為![]()
當![]() 時,
時,![]() ,
,
∴當![]() 取最小值時,點
取最小值時,點![]() 的坐標為
的坐標為![]() .
.
在![]() 中,
中,![]() ,
,![]() .
.
∴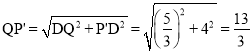 .
.
過點![]() 作
作![]() ,垂足為點
,垂足為點![]() ,
,
∵![]() ,
,
∴
∴當![]() 取最小值時,點
取最小值時,點![]() 到直線
到直線![]() 的距離為
的距離為![]() .
.
②(a)如圖3中,當點M在線段EA的延長線上,點N在線段AE時,
作MH⊥OB于H,GK⊥EB于K,
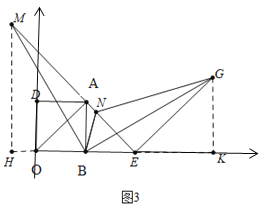
由翻折可知:∠MBN=∠NBG=45°,BM=BG,
∴∠MBG=90°,
∵∠MHB=∠K=90°,
∴∠MBH+∠GBK=90°,∠HBM+∠BMH=90°,
∴∠BMH=∠GBK,
∴△BMH≌△GBK,
∴HM=EH=BK,BH=GK,
∴BH=EK=GK,
∴∠GEK=∠BEA=45°,
∴∠MEG=90°,
∵NE:EG=5:12,設NE=5k,EG=12k,則MN=NG=13k,EM=18k,
∴BH=GK=EK=6![]() k,EH=MH=9
k,EH=MH=9![]() k,
k,
∵HE=BH+BE,
∴9![]() k=6
k=6![]() k+3,
k+3,
∴k=![]() ,∴EH=MH=9,
,∴EH=MH=9,
∴OH=3.∴點![]() 的坐標為
的坐標為![]()
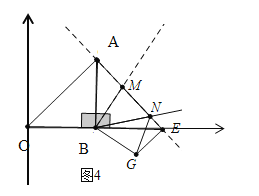
(b)如圖4中,當點M,N在線段EA上時,同法可得:點![]() 的坐標為
的坐標為![]() .
.
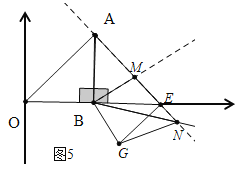
(c)如圖5中,當點M在線段EA上,點N在AE的延長線上時,同法可得:點![]() 的坐標為
的坐標為![]() .
.
綜上所述,點![]() 的坐標
的坐標![]() 或
或![]() 或
或![]() .
.


科目:初中數(shù)學 來源: 題型:
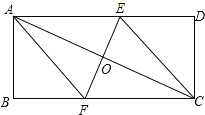
【題目】如圖,矩形ABCD的對角線AC的垂直平分線EF與AD、AC、BC分別交于點E、O、F.
(1)求證:四邊形AFCE是菱形;
(2)若AB=5,BC=12,求菱形AFCE的面積.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】我市在創(chuàng)建全國文明城市過程中,決定購買A、B兩種樹苗對某路段道路進行綠化改造,已知購買A種樹苗5棵,B種樹苗3棵,需要840元;購買A種樹苗3棵,B種樹苗5棵,需要760元.
(1)求購買A、B兩種樹苗每棵各需多少元?
(2)考慮到綠化效果和資金周轉,購進A種樹苗不能少于30棵,且用于購買這兩種樹苗的資金不能超過10000元,現(xiàn)需購進這兩種樹苗共100棵,怎樣購買所需資金最少?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在矩形ABCD中,AB<AD,對角線AC,BD相交于點O,動點P由點A出發(fā),沿AB→BC→CD向點D運動.設點P的運動路程為x,△AOP的面積為y,y與x的函數(shù)關系圖象如圖②所示,則AD邊的長為( )
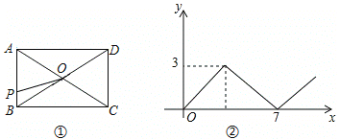
A.3B.4C.5D.6
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
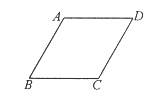
【題目】如圖,在菱形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是這個菱形內(nèi)部或邊上的一點,若以點
是這個菱形內(nèi)部或邊上的一點,若以點![]() ,
,![]() ,
,![]() 為頂點的三角形是等腰三角形,則
為頂點的三角形是等腰三角形,則![]() ,
,![]() (
(![]() ,
,![]() 兩點不重合)兩點間的最短距離為( )
兩點不重合)兩點間的最短距離為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】下面是小明主設計的“作一個含30°角的直角三角形”的尺規(guī)作圖過程.
已知:直線l.
![]()
求作:△ABC,使得∠ACB=90°,∠ABC=30°.
作法:如圖,
![]()
①在直線l上任取兩點O,A;
②以點O為圓心,OA長為半徑畫弧,交直線l于點B;
③以點A為圓心,AO長為半徑畫弧,交![]() 于點C;
于點C;
④連接AC,BC.
所以△ABC就是所求作的三角形.
根據(jù)小明設計的尺規(guī)作圖過程:
(1)使用直尺和圓規(guī),補全圖形;(保留作圖痕跡)
(2)完成下面的證明.
證明:在⊙O中,AB為直徑,
∴∠ACB=90°(① ),(填推理的依據(jù))
連接OC
∵OA=OC=AC,
∴∠CAB=60°,
∴∠ABC=30°(② ),(填推理的依據(jù))
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在正方形ABCD中,E為BC邊上一動點(不與點B、C重合),延長AE到點F,連接BF,且∠AFB=45°,G為DC邊上一點,且DG=BE,連接DF,點F關于直線AB的對稱點為M,連接AM、BM.
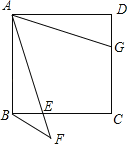
(1)依據(jù)題意,補全圖形;
(2)求證:∠DAG=∠MAB;
(3)用等式表示線段BM、DF與AD的數(shù)量關系,并證明.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,以A(0, ![]() )為圓心的圓與x軸相切于坐標原點O,與y軸相交于點B,弦BD的延長線交x軸的負半軸于點E,且∠BEO=60°,AD的延長線交x軸于點C.
)為圓心的圓與x軸相切于坐標原點O,與y軸相交于點B,弦BD的延長線交x軸的負半軸于點E,且∠BEO=60°,AD的延長線交x軸于點C.
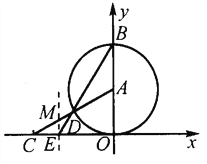
(1)分別求點E、C的坐標;
(2)求經(jīng)過A、C兩點,且以過E而平行于y軸的直線為對稱軸的拋物線的函數(shù)解析式;
(3)設拋物線的對稱軸與AC的交點為M,試判斷以M點為圓心,ME為半徑的圓與⊙A的位置關系,并說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com