
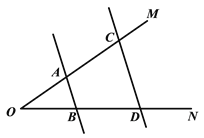
【題目】問題情境:如圖,![]() ∥
∥![]() ,
,![]() ,
,![]() ,求
,求![]() 的度數(shù).
的度數(shù).
小明的思路是過點(diǎn)![]() 作
作![]() ∥
∥![]() ,通過平行線的性質(zhì)來求
,通過平行線的性質(zhì)來求![]() .
.

(1)按照小明的思路,求![]() 的度數(shù);
的度數(shù);
(2)問題遷移:如圖,![]() ∥
∥![]() ,點(diǎn)
,點(diǎn)![]() 在射線
在射線![]() 上運(yùn)動(dòng),記
上運(yùn)動(dòng),記![]() ,
,![]() ,當(dāng)點(diǎn)
,當(dāng)點(diǎn)![]() 在
在![]() 、
、![]() 兩點(diǎn)之間運(yùn)動(dòng)時(shí),問
兩點(diǎn)之間運(yùn)動(dòng)時(shí),問![]() 與
與![]() 、
、![]() 之間有何數(shù)量關(guān)系?請(qǐng)說明理由;
之間有何數(shù)量關(guān)系?請(qǐng)說明理由;

(3)在(2)的條件下,如果點(diǎn)![]() 不在
不在![]() 、
、![]() 兩點(diǎn)之間運(yùn)動(dòng)時(shí)(點(diǎn)
兩點(diǎn)之間運(yùn)動(dòng)時(shí)(點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 、
、![]() 、
、![]() 三點(diǎn)不重合),請(qǐng)直接寫出
三點(diǎn)不重合),請(qǐng)直接寫出![]() 與
與![]() 、
、![]() 之間的數(shù)量關(guān)系.
之間的數(shù)量關(guān)系.
【答案】(1)110°(2)![]() (3)①當(dāng)點(diǎn)
(3)①當(dāng)點(diǎn)![]() 在
在![]() 左側(cè)時(shí),
左側(cè)時(shí),![]() ; ②當(dāng)點(diǎn)
; ②當(dāng)點(diǎn)![]() 在
在![]() 右側(cè)時(shí),
右側(cè)時(shí),![]()
【解析】分析:(1)過P作PE∥AB,通過平行線性質(zhì)可得∠A+∠APE=180°,∠C+∠CPE=180°再代入∠PAB=130°,∠PCD=120°可求∠APC即可;
(2)過P作PE∥AD交AC于E,推出AB∥PE∥DC,根據(jù)平行線的性質(zhì)得出∠α=∠APE,∠β=∠CPE,即可得出答案;
(3)分兩種情況:P在BD延長(zhǎng)線上;P在DB延長(zhǎng)線上,分別畫出圖形,根據(jù)平行線的性質(zhì)得出∠α=∠APE,∠β=∠CPE,即可得出答案.
詳解:∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180,∠C+∠CPE=180,
∵∠PAB=130,∠PCD=120,
∴∠APE=50,∠CPE=60,
∴∠APC=∠APE+∠CPE=110.
(2)∠APC=∠α+∠β,
理由:如圖2,過P作PE∥AB交AC于E,
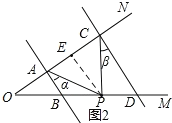
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
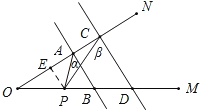
(3)如圖所示,當(dāng)P在BD延長(zhǎng)線上時(shí),∠CPA=∠α∠β;

如圖所示,當(dāng)P在DB延長(zhǎng)線上時(shí),∠CPA=∠β∠α.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】三十億八千零五萬二千零六十,這個(gè)數(shù)寫作_______,省略萬位后面的尾數(shù)約是______萬.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】對(duì)于式子 -(-8)下列理解:①可表示-8的相反數(shù);②可表示-1與-8的積;③可表示-8的絕對(duì)值;④運(yùn)算結(jié)果是8.其中理解錯(cuò)誤的個(gè)數(shù)有( )
A.3B.2C.1D.0
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】四邊形ABCD為菱形,BD為對(duì)角線,在對(duì)角線BD上任取一點(diǎn)E,連接CE,把線段CE繞點(diǎn)C順時(shí)針旋轉(zhuǎn)得到線段CF,使得∠ECF=∠BCD ,點(diǎn)E的對(duì)應(yīng)點(diǎn)為點(diǎn)F,連接DF.
(1)如圖1,求證:BE=DF;
(2)如圖2,若DF=![]() CF=10, ∠DFC=2∠BDC,求菱形ABCD的邊長(zhǎng).
CF=10, ∠DFC=2∠BDC,求菱形ABCD的邊長(zhǎng).


查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形網(wǎng)格中的每個(gè)小正方形邊長(zhǎng)都是![]() ,每個(gè)小格的頂點(diǎn)叫做格點(diǎn),以格點(diǎn)為頂點(diǎn)分別按下列要求畫三角形.
,每個(gè)小格的頂點(diǎn)叫做格點(diǎn),以格點(diǎn)為頂點(diǎn)分別按下列要求畫三角形.
(![]() )畫一個(gè)三角形,使它的三邊長(zhǎng)都是有理數(shù).
)畫一個(gè)三角形,使它的三邊長(zhǎng)都是有理數(shù).
(![]() )畫一個(gè)直角三角形,使它們的三邊長(zhǎng)都是無理數(shù).
)畫一個(gè)直角三角形,使它們的三邊長(zhǎng)都是無理數(shù).
(![]() )畫出與
)畫出與![]() 成軸對(duì)稱且與
成軸對(duì)稱且與![]() 有公共點(diǎn)的格點(diǎn)三角形(畫出一個(gè)即可).
有公共點(diǎn)的格點(diǎn)三角形(畫出一個(gè)即可).



查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知AB是⊙O的直徑,PB是⊙O的切線,C是⊙O上的點(diǎn),AC∥OP,M是直徑AB上的動(dòng)點(diǎn),A與直線CM上的點(diǎn)連線距離的最小值為d,B與直線CM上的點(diǎn)連線距離的最小值為f.
(1)求證:PC是⊙O的切線;
(2)設(shè)OP=![]() AC,求∠CPO的正弦值;
AC,求∠CPO的正弦值;
(3)設(shè)AC=9,AB=15,求d+f的取值范圍.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】我國古代數(shù)學(xué)的許多創(chuàng)新和發(fā)展都位居世界前列,如南宋數(shù)學(xué)家楊輝(約13世紀(jì))所著的《詳解九章算術(shù)》一書中,用如圖的三角形解釋二項(xiàng)式乘方(a+b)n的展開式的各項(xiàng)系數(shù),此三角形稱為“楊輝三角”.

根據(jù)“楊輝三角”請(qǐng)計(jì)算(a+b)64的展開式中第三項(xiàng)的系數(shù)為( )
A. 2016 B. 2017 C. 2018 D. 2019
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點(diǎn)B、D、C、F在一條直線上,且BD=FC,AB=EF.

(1)請(qǐng)你只添加一個(gè)條件(不再加輔助線),使△ABC≌△EFD,你添加的條件是 ;
(2)添加了條件后,證明△ABC≌△EFD.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某班為了解學(xué)生一學(xué)期做義工的時(shí)間情況,對(duì)全班50名學(xué)生進(jìn)行調(diào)查,按做義工的時(shí)間![]() (單位:小時(shí)),將學(xué)生分成五類:
(單位:小時(shí)),將學(xué)生分成五類: ![]() 類(
類(![]() ),
),![]() 類(
類(![]() ),
),![]() 類(
類(![]() ),
),![]() 類(
類(![]() ),
),![]() 類(
類(![]() ),繪制成尚不完整的條形統(tǒng)計(jì)圖如圖11.
),繪制成尚不完整的條形統(tǒng)計(jì)圖如圖11.

根據(jù)以上信息,解答下列問題:
(1)![]() 類學(xué)生有 人,補(bǔ)全條形統(tǒng)計(jì)圖;
類學(xué)生有 人,補(bǔ)全條形統(tǒng)計(jì)圖;
(2)![]() 類學(xué)生人數(shù)占被調(diào)查總?cè)藬?shù)的 %;
類學(xué)生人數(shù)占被調(diào)查總?cè)藬?shù)的 %;
(3)從該班做義工時(shí)間在![]() 的學(xué)生中任選2人,求這2人做義工時(shí)間都在
的學(xué)生中任選2人,求這2人做義工時(shí)間都在![]() 中的概率.
中的概率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com