
【題目】如圖,拋物線y=ax2+bx﹣3a(a≠0)與x軸交于點A(﹣1,0)和點B,與y軸交于點C(0,2),連接BC.
(1)求該拋物線的解析式和對稱軸,并寫出線段BC的中點坐標;
(2)將線段BC先向左平移2個單位長度,再向下平移m個單位長度,使點C的對應(yīng)點C1恰好落在該拋物線上,求此時點C1的坐標和m的值;
(3)若點P是該拋物線上的動點,點Q是該拋物線對稱軸上的動點,當以P,Q,B,C四點為頂點的四邊形是平行四邊形時,求此時點P的坐標.
【答案】
(1)
解:∵拋物線y=ax2+bx﹣3a(a≠0)與x軸交于點A(﹣1,0)和點B,與y軸交于點C(0,2),
∴ ![]() ,
,
解得  .
.
∴拋物線的解析式為y=﹣ ![]() x2+
x2+ ![]() x+2=﹣
x+2=﹣ ![]() (x﹣1)2+2
(x﹣1)2+2 ![]() ,
,
∴對稱軸是x=1,
∵1+(1+1)=3,
∴B點坐標為(3,0),
∴BC的中點坐標為(1.5,1)
(2)
解:∵線段BC先向左平移2個單位長度,再向下平移m個單位長度,使點C的對應(yīng)點C1恰好落在該拋物線上,
∴點C1的橫坐標為﹣2,
當x=﹣2時,y=﹣ ![]() ×(﹣2)2+
×(﹣2)2+ ![]() ×(﹣2)+2=﹣
×(﹣2)+2=﹣ ![]() ,
,
∴點C1的坐標為(﹣2,﹣ ![]() ),
),
m=2﹣(﹣ ![]() )=5
)=5 ![]()
(3)
解:①若BC為平行四邊形的一邊,
∵BC的橫坐標的差為3,
∵點Q的橫坐標為1,
∴P的橫坐標為4或﹣2,
∵P在拋物線上,
∴P的縱坐標為﹣3 ![]() ,
,
∴P1(4,﹣3 ![]() ),P2(﹣2,﹣3
),P2(﹣2,﹣3 ![]() );
);
②若BC為平行四邊形的對角線,
則BC與PQ互相平分,
∵點Q的橫坐標為1,BC的中點坐標為(1.5,1),
∴P點的橫坐標為1.5+(1.5﹣1)=2,
∴P的縱坐標為﹣ ![]() ×22+
×22+ ![]() ×2+2=2,
×2+2=2,
∴P3(2,2).
綜上所述,點P的坐標為:P1(4,﹣3 ![]() ),P2(﹣2,﹣3
),P2(﹣2,﹣3 ![]() ),P3(2,2)
),P3(2,2)
【解析】(1)把點A(﹣1,0)和點C(0,2)的坐標代入所給拋物線可得a、b的值,進而得到該拋物線的解析式和對稱軸,再求出點B的坐標,根據(jù)中點坐標公式求出線段BC的中點坐標即可;(2)根據(jù)平移的性質(zhì)可知,點C的對應(yīng)點C1的橫坐標為﹣2,再代入拋物線可求點C1的坐標,進一步得到m的值;(3)B、C為定點,可分BC為平行四邊形的一邊及對角線兩種情況探討得到點P的坐標.
【考點精析】解答此題的關(guān)鍵在于理解二次函數(shù)的性質(zhì)的相關(guān)知識,掌握增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小.


科目:初中數(shù)學(xué) 來源: 題型:
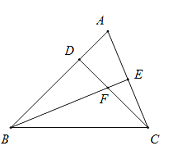
【題目】在△ABC中,BA=BC,BE平分∠ABC,CD⊥BD,且CD=BD.
(1)求證:BF=AC;
(2)若AD=![]() ,求CF的長.
,求CF的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
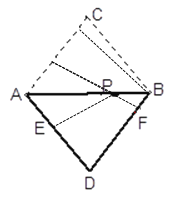
【題目】如圖,在△ABC中,AC=BC=5,AB=6,將它沿AB翻折得到△ABD,點P、E、F分別為線段AB、AD、DB的任意點,則PE+PF的最小值是________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】計算下列各題
(1)計算: ![]() ﹣(
﹣( ![]() )﹣1+(π﹣
)﹣1+(π﹣ ![]() )0﹣(﹣1)100;
)0﹣(﹣1)100;
(2)已知|a+1|+(b﹣3)2=0,求代數(shù)式( ![]() ﹣
﹣ ![]() )÷
)÷ ![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在正方形ABCD中,點E是對角線AC上一點,且CE=CD,過點E作EF⊥AC交AD于點F,連接BE. 
(1)求證:DF=AE;
(2)當AB=2時,求BE2的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=BC,點D在AB的延長線上. 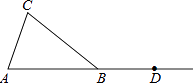
(1)利用尺規(guī)按下列要求作圖,并在圖中標明相應(yīng)的字母(保留作圖痕跡,不寫作法). ①作∠CBD的平分線BM;
②作邊BC上的中線AE,并延長AE交BM于點F.
(2)由(1)得:BF與邊AC的位置關(guān)系是 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
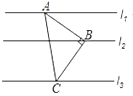
【題目】如圖,Rt△ABC中,∠ABC=90°,AB=BC,直線l1、l2、l3分別通過A、B、C三點,且l1∥l2∥l3.若l1與l2的距離為4,l2與l3的距離為6,則Rt△ABC的面積為___________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩同學(xué)的家與學(xué)校的距離均為3000米.甲同學(xué)先步行600米,然后乘公交車去學(xué)校,乙同學(xué)騎自行車去學(xué)校.已知甲步行速度是乙騎自行車速度的![]() ,公交車的速度是乙騎自行車速度的2倍.甲乙兩同學(xué)同時從家出發(fā)去學(xué)校,結(jié)果甲同學(xué)比乙同學(xué)早到2分鐘.乙騎自行車的速度是( )米/分.
,公交車的速度是乙騎自行車速度的2倍.甲乙兩同學(xué)同時從家出發(fā)去學(xué)校,結(jié)果甲同學(xué)比乙同學(xué)早到2分鐘.乙騎自行車的速度是( )米/分.
A. 600 B. 400 C. 300 D. 150
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,D 是 AB 邊上的中點,將△ABC 沿過點 D 的直線折疊,DE 為折痕,使點 A 落在 BC 上 F處,若∠B=40°,則∠EDF=_____度.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com