Question

若關于x的方程rx²-（2r+7）x+r+7=0的根是正整數，則整數r的值可以是    ．

Answer 1

【答案】分析：利用根與系數的關系，得出方程的根，在進行分析得出整數解．
解答：解：當r=0時，方程為-7x+7=0顯然符合題意
當r≠0時，x₁+x₂=
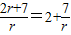
x₁x₂=，
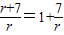
∴x₁x₂-（x₁+x₂）=-1
（x₁-1）（x₂-1）=0
∴x₁=1，x₂=1．
可知方程必有一根為1，則另一根為1+，是正整數，
∴r是7的正約數，即r=7或1，
∴r=7，0，1
故填：7或0或1．
點評：此題主要考查了一元二次方程根與系數的應用，題目比較新穎．