
分析 將原方程變現為一般式,根據方程有兩個整數根即可得出△=4×(5p+1)為完全平方數,設5p+1=n2,根據5p=n2-1=(n-1)(n+1),即可得出n-1、n+1中至少有一個是5的倍數,即n=5k±1(k為正整數),結合p為素數即可求出p、k的值,將p的值代入原方程,再解方程即可得出結論.
解答 解:原方程可變形為x2-4px+4p2-5p-1=0,
∵方程的兩根均為整數,
∴△=(-4p)2-4×(4p2-5p-1)=4×(5p+1)為完全平方數,
∴5p+1為完全平方數.
設5p+1=n2,
∵p為素數,
∴p≥2,
∴n≥4,且n為整數.
∵5p=n2-1=(n-1)(n+1),
∴n-1、n+1中至少有一個是5的倍數,即n=5k±1(k為正整數),
∴5p+1=25k2±10k+1,
∴p=k(5k±2).
∵p為素數,5k±2>1,
∴k=1,p=3或7.
當p=3時,原方程為x2-12x+20=0,
解得:x1=2,x2=10;
當p=7時,原方程為x2-28x+160=0
解得:x1=8,x2=20.
點評 本題考查了根的判別式以及解一元二次方程,根據方程有兩個整數根得出△=4×(5p+1)為完全平方數是解題的關鍵.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:選擇題
| A. | 求兩個有理數的絕對值,并比較大小 | |
| B. | 確定和的符號 | |
| C. | 觀察兩個有理數的符號,并作出一些判斷 | |
| D. | 用較大的絕對值減去較小的絕對值 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
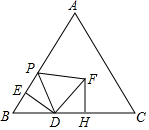 如圖,在等邊△ABC中,AB=10,BD=4,BE=2,點P從點E出發沿EA方向運動,連接PD,以PD為邊,在PD右側按如圖方式作等邊△DPF.
如圖,在等邊△ABC中,AB=10,BD=4,BE=2,點P從點E出發沿EA方向運動,連接PD,以PD為邊,在PD右側按如圖方式作等邊△DPF.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com